Question

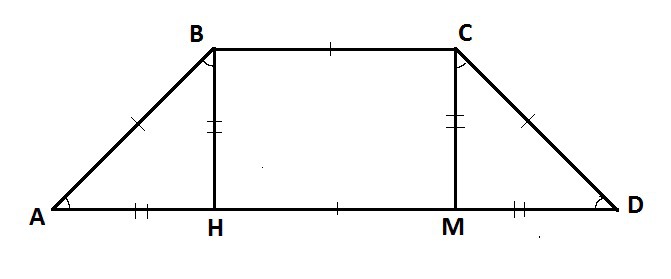
Равнобедренная трапеция АВСД, АВ=ВС=СД= 5. Угол АВС 135 градусов. Из вершины С опушена высота СН к нижнему основанию АД. Найдите длину большего основания АД.

Answer 1

трапеция равнобедренная, значит ∠ABC = ∠BCD,  ∠BAD = ADC;
∠MCD = ∠ABH = 135° - 90° = 45°
ΔABH и ΔMCD , прямоугольные и равнобедренные, так так у них два угла по 45°, и  так же равны
MD=AH, найдем MD:
ΔMCD: sin∠C = $frac{MD}{CD}$
MD = sin∠C*CD = $frac{ 5sqrt{2} }{2}$
HM=BC
AD = AH + MD + HM = 2AH + HM = $frac{ 2*5sqrt{2} }{2} + 5 = 5 sqrt{2} + 5 = 5( sqrt{2} + 1)$