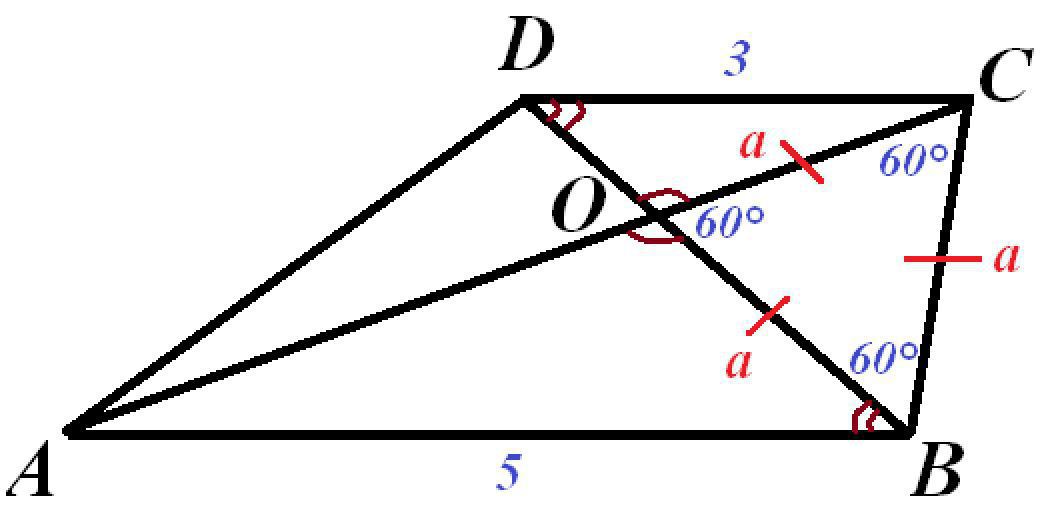
В трапеции ABCD с основаниями AB и CD диагонали AC и BD пересекаются в точке О, причем треугольник BOC равносторонний. Известно, что АВ = 5, CD = 3. Найдите длину стороны BC.
Ответы
Ответ дал:
0
Ситуация с чертежом в данной задаче нетипичная для школы, т.к. боковые стороны трапеции имеют "однобокий уклон" (это не термин).
Т.к. при пересечении диагоналей АC и BD в точке О образовался равносторонний Δ ВОС, то у него все углы по 60°. Следовательно, ∠АОB = 120° (смежный с ∠ВОС=60°).
ΔCOD и ΔAOB подобны по двум углам (отмечены дугами на рисунке).
Запишем отношение сходственных сторон:

Обозначим CB=CO=OB=a.

Отсюда
В Δ АОВ по теореме косинусов АВ² = АО² + ОВ² - 2АО·ОВ·cos∠O.






Ответ:
Т.к. при пересечении диагоналей АC и BD в точке О образовался равносторонний Δ ВОС, то у него все углы по 60°. Следовательно, ∠АОB = 120° (смежный с ∠ВОС=60°).
ΔCOD и ΔAOB подобны по двум углам (отмечены дугами на рисунке).
Запишем отношение сходственных сторон:
Обозначим CB=CO=OB=a.
Отсюда
В Δ АОВ по теореме косинусов АВ² = АО² + ОВ² - 2АО·ОВ·cos∠O.
Ответ:
Приложения:

Ответ дал:
0
спасибо
Вас заинтересует
7 лет назад
10 лет назад
10 лет назад
10 лет назад