Докажите, что наклонная асимптота графика функции  параллельна касательной к графику
параллельна касательной к графику  в точке с абциссой
в точке с абциссой 
Заранее огромное спасибо!!
Ответы
Ответ дал:
0
наклонной асимптотой и касательной является прямая вида:
у=kх+b, где k-угловой коэффициент прямой.
Геометрический смысл производной:
k=tgα=f '(x₀)
чтобы прямые были параллельными, необходимо и достаточно, чтобы соответственные углы были равны, то есть:
α=β ⇒ tgα=tgβ ⇒ k₁=k₂
если функция задаётся дробью в которой в числителе и знаменателе стоят многочлены, то наклонную асимптоту можно найти делением числителя на знаменатель столбиком и то что получится в частном и будет наклонная асимптота (см.фото 1) у=kx+b
y=x+2 ⇒ k₁=1
или в общем виде найти через предел (см. фото 2)

Итак, k₁=k₂=1, следовательно данные наклонная асимптота и касательная параллельны - ч.т.д
у=kх+b, где k-угловой коэффициент прямой.
Геометрический смысл производной:
k=tgα=f '(x₀)
чтобы прямые были параллельными, необходимо и достаточно, чтобы соответственные углы были равны, то есть:
α=β ⇒ tgα=tgβ ⇒ k₁=k₂
если функция задаётся дробью в которой в числителе и знаменателе стоят многочлены, то наклонную асимптоту можно найти делением числителя на знаменатель столбиком и то что получится в частном и будет наклонная асимптота (см.фото 1) у=kx+b
y=x+2 ⇒ k₁=1
или в общем виде найти через предел (см. фото 2)
Итак, k₁=k₂=1, следовательно данные наклонная асимптота и касательная параллельны - ч.т.д
Приложения:
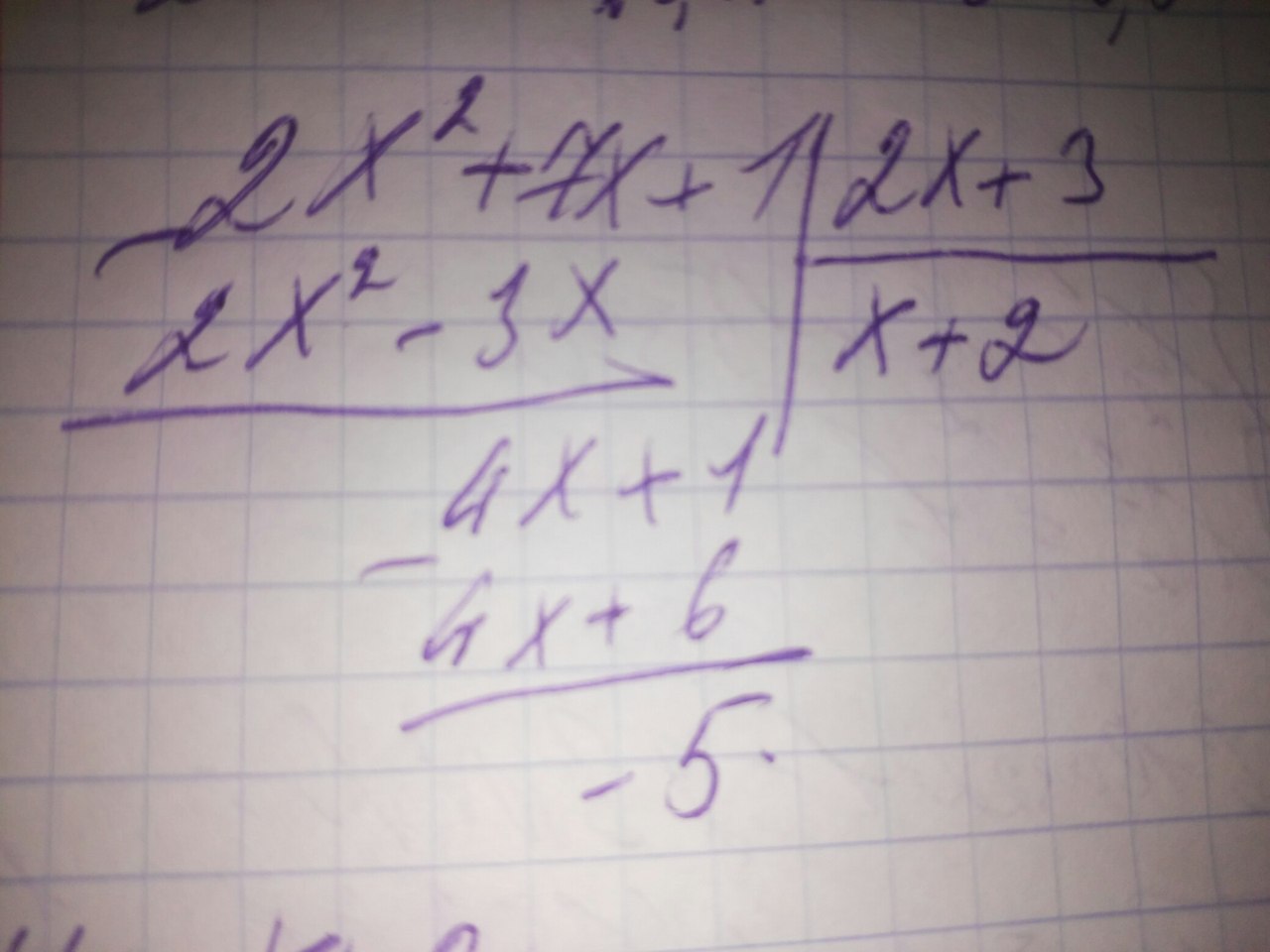
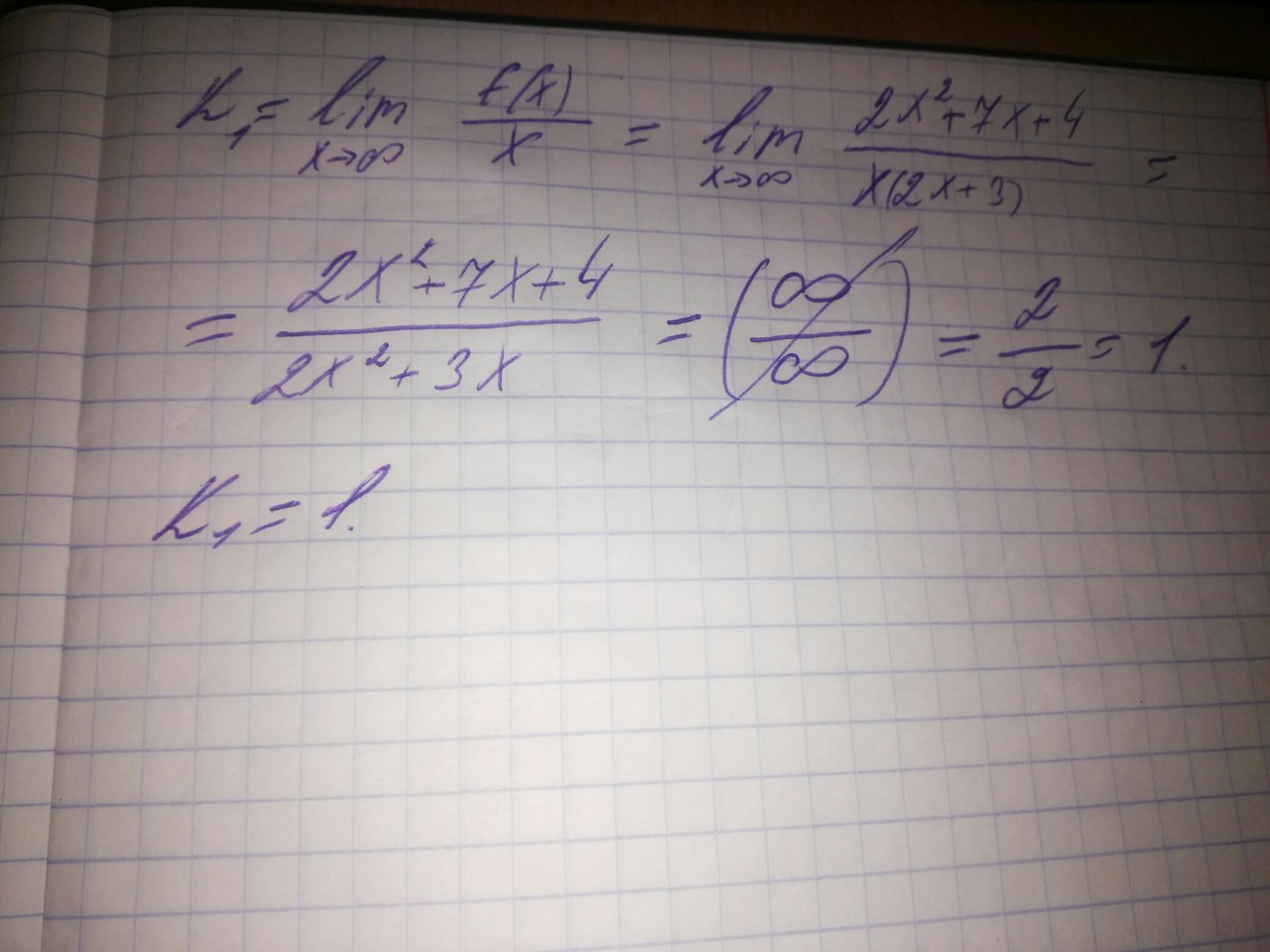
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад