Question

Какая облась значения функции? (ФОТО)

Answer 1

Сначала рассмотрим область определения функции f(x):
5-4x-x^2>=0,
-(x+5)(x-1)>=0
x∈[-5;1]
Теперь найдем производную для определения промежутков возрастания и убывания.
$f'(x)= frac{ frac{1}{2 sqrt{5-4x-x^2} }(-4-2x)(x+2) - sqrt{5-4x-x^2} }{(x+2)^2}=$
$-frac{frac{(x+2)^2 }{ sqrt{5-4x-x^2} } +sqrt{5-4x-x^2}}{(x+2)^2} textless 0$
Поэтому функция постоянно убывает. Но теперь рассмотрим ее вертикальную асимптоту x=-2. Найдем левосторонний и правосторонний пределы функции f(x) в точке x=-2:
$lim_{x to -2-0} f(x)= lim_{x to -2-0} frac{ sqrt{5-4x-x^2} }{x+2} =[ frac{3}{-0} ] =-infty$
$lim_{x to -2+0} f(x)= lim_{x to -2+0} frac{ sqrt{5-4x-x^2} }{x+2} =[ frac{3}{0} ] =infty$
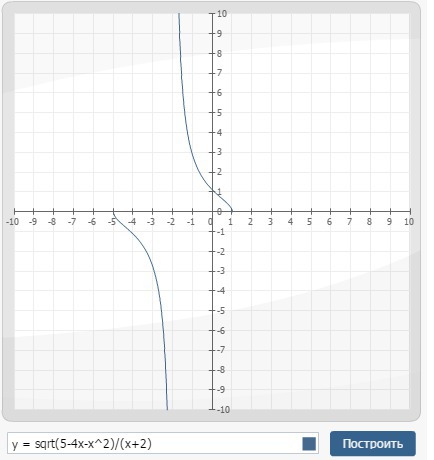
Таким образом, при x∈[-5;-2) функция изменяется от 0 до -∞. При x∈(-2;1] функция изменяется от +∞ до 0.
Область значений функции получается (-∞;+∞). Для наглядности прилагаю рисунок.