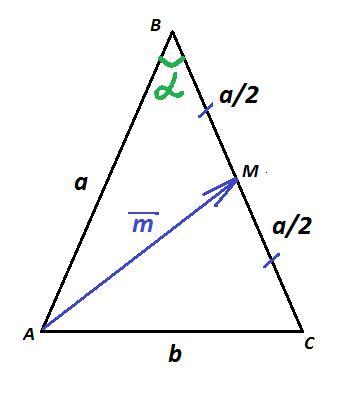
В равнобедренном треугольнике с боковой стороной а и основанием b найдите длину вектора, совпадающего с медианой, проведенной к боковой стороне.
Ответы
Ответ дал:
0
Так как вектор совпадает с медианой, то можно воспользоваться готовой формулой длины медианы
Либо можно решить задачу, используя теорему косинусов
ΔABC : b² = a² + a² - 2a·a·cos α
2a²cos α = 2a² - b²
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад