Ответы
Ответ дал:
0
Доп. построение:
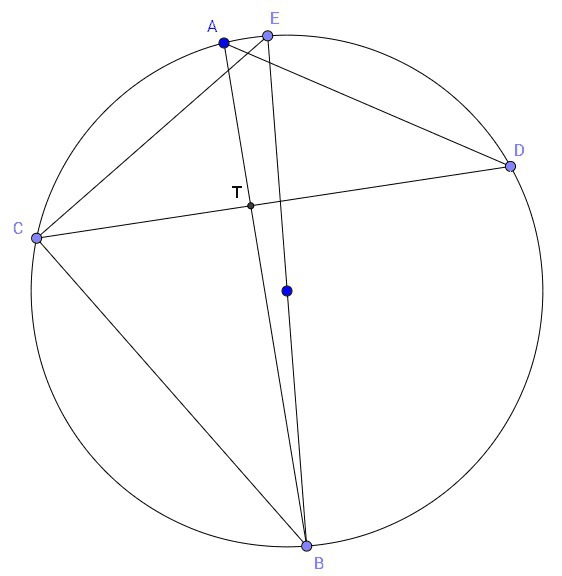
CE = AD
∪CE = ∪AD (дуги, стягивающие равные хорды)
∪CA + ∪AE = ∪AE + ∪ED <=> ∪CA = ∪ED
∠ADC = ∠DCE (углы, опирающиеся на равные дуги)
∠ADC = ∠ABC (опираются на дугу CA)
∠DCE = ∠ABC
∠BCD + ∠ABC = 90 (т.к. ∠CTB = 90)
∠BCD + ∠DCE = 90
∠BCE = 90
EB - диаметр окружности
CE = AD = 6
BC = 8
EB = √(36+64) = 10
Радиус окружности = 5
CE = AD
∪CE = ∪AD (дуги, стягивающие равные хорды)
∪CA + ∪AE = ∪AE + ∪ED <=> ∪CA = ∪ED
∠ADC = ∠DCE (углы, опирающиеся на равные дуги)
∠ADC = ∠ABC (опираются на дугу CA)
∠DCE = ∠ABC
∠BCD + ∠ABC = 90 (т.к. ∠CTB = 90)
∠BCD + ∠DCE = 90
∠BCE = 90
EB - диаметр окружности
CE = AD = 6
BC = 8
EB = √(36+64) = 10
Радиус окружности = 5
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад