диагонали выпуклого четырехугольника равны m и n. Отрезки, соединяющие середины противолежащих сторон, равны друг другу. Докажите, что его площадь равна 0,5mn.
Ответы
Ответ дал:
0
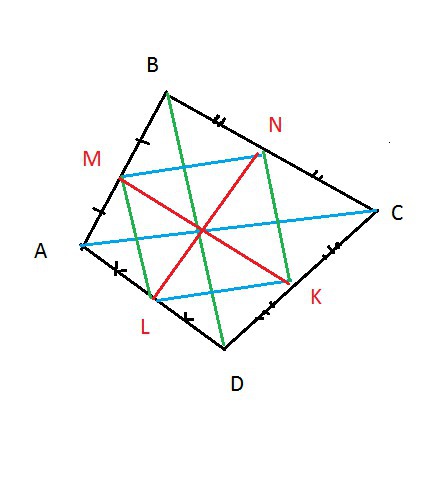
Cм. рисунок в приложении.
М,N,K,L- середины сторон четырехугольника АВСD.
АС=m; BD=n.
По свойству средней линии треугольника
ML=NK=AC/2
MN=LK=BD/2
Значит противоположные стороны четырехугольника MNKL равны.
Диагонали этого четырехугольника MK и LN равны по условию.
Значит,MNKL - прямоугольник.
MN⊥NK ⇒ AC⊥BD
S (АВСD)=AC·BD·sin90°/2=mn/2
М,N,K,L- середины сторон четырехугольника АВСD.
АС=m; BD=n.
По свойству средней линии треугольника
ML=NK=AC/2
MN=LK=BD/2
Значит противоположные стороны четырехугольника MNKL равны.
Диагонали этого четырехугольника MK и LN равны по условию.
Значит,MNKL - прямоугольник.
MN⊥NK ⇒ AC⊥BD
S (АВСD)=AC·BD·sin90°/2=mn/2
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад