Ответы
Ответ дал:
0
Это степенной ряд, найдём его радиус сходимости.
Согласно признаку Даламбера.
Так как радиус сходимости степенного ряда равен 1, то при |x| >1, ряд расходится.
Проверим сходимость в точках x = 1 и x = -1.
При x = 1, ряд (*) — расходится (так как не выполняется необходимое условие сходимости числового ряда).
При x = -1, ряд (*) – расходится (так как не выполняется необходимое условие сходимости числового ряда).
Ряд сходится при |x| < 1.
- разложение в ряд Маклорена функции
См. дальнейшее решение во вложении.
при
Приложения:
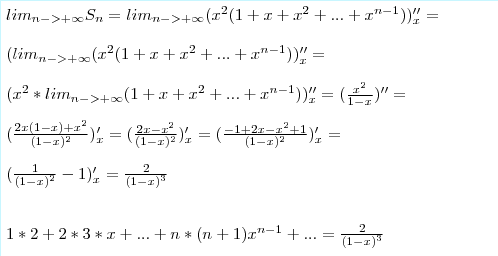
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад