Question

Очень срочно нужно решить на этом листе, домашнюю работу, пожалуйста объясните как это делать , буду очень благодарна!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1

Answer 1

Ну смотри.
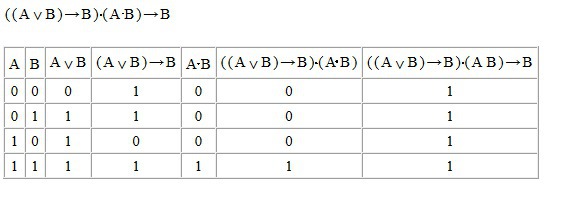
В первом случае импликация. Будет значение 0 только в том случае, если
((A∨B)→B)&(A&B)=1
а B=0;
Но если B=0, то ((A∨B)→B)&(A&B) = 0 (т.к (A&B)=0);
Значит это выражение тождественно истинное. Т.е. Всегда принимает значение 1.


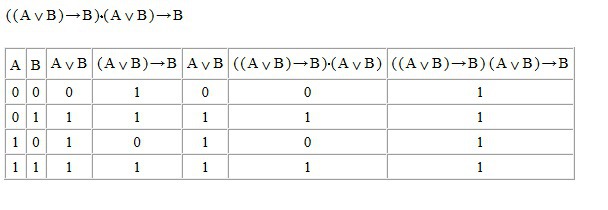
Во втором случае все примерно так же.
Будет значение 0 только в том случае, если
((A∨B)→B)&(A∨B)=1
а B=0;
Тогда (A∨B)=1 => A=1,
но тогда ((A∨B)→B)=0 (т.к  (A∨B)=1; 1→0=0)
Значит и это выражение тождественно истинное. Т.е. Всегда принимает значение 1.

Можно упростить эти выражения, чтобы было наглядно.
А можно просто построить таблицы истинности для каждого случая и лишний раз убедиться.
Оставлю в прикрепленных.


Ответ: 1; 1