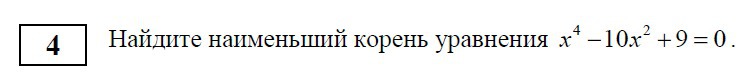Ответы
Ответ дал:
0
x^4-10x^2+9=0
x1^2=(10+sqr(100-36))/2=9
x2^2=(10-8)/2=1
x1;2=3;-3
x3,4=1;-1
Ответ: -3
x1^2=(10+sqr(100-36))/2=9
x2^2=(10-8)/2=1
x1;2=3;-3
x3,4=1;-1
Ответ: -3
Ответ дал:
0
Примем  Тогда заданное уравнение принимает вид
Тогда заданное уравнение принимает вид  Решая это уравнение относительно неизвестной величины
Решая это уравнение относительно неизвестной величины  получим
получим 
 Тогда
Тогда 

Ответ дал:
0
Прошу извинить за ошибку в наборе. Разумеется, t2=(10+8)/2=9.
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад