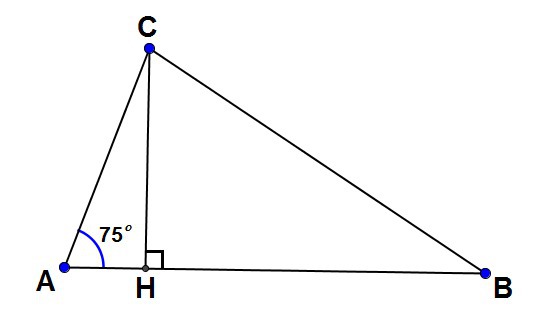
В треугольнике ABC высота CH=5, сторона AB=10, а угол BAC = 75. Найдите угол ABC (в градусах).
Приложения:
Ответы
Ответ дал:
0
Ну, может, я ошибаюсь, но угол в 75 градусов тут вообще не нужен.
Рассмотрит треугольник СНВ:
Угол Н= 90 ( по условию), значит
СН- высота, значит
Т.к. СВ=10( по условию,
а СН= 5( по условию),
То угол АВС= 30 градусов( свойство)
Как-то слишком просто, чувствую подвох
Рассмотрит треугольник СНВ:
Угол Н= 90 ( по условию), значит
СН- высота, значит
Т.к. СВ=10( по условию,
а СН= 5( по условию),
То угол АВС= 30 градусов( свойство)
Как-то слишком просто, чувствую подвох
Ответ дал:
0
я поняла
Ответ дал:
0
я ошиблась, не то отметила себе на рисунке
Ответ дал:
0
ты не так решила?)
Ответ дал:
0
нет
Ответ дал:
0
Сейчас опять попробую
Ответ дал:
0
Решение:
В треугольнике АВС:
СН - высота, СН=5, АВ=10, угол ВАС=75град.
Если СН=5, АВ=10, угол СН=90град, то по правилу (катет, лежащий напротив угла в 30 градусов равен половине гипотенузы), угол АВС=30град.
Ответ: 30град.
В треугольнике АВС:
СН - высота, СН=5, АВ=10, угол ВАС=75град.
Если СН=5, АВ=10, угол СН=90град, то по правилу (катет, лежащий напротив угла в 30 градусов равен половине гипотенузы), угол АВС=30град.
Ответ: 30град.
Ответ дал:
0
Это крайне не логично! если бы НВ было равно 6, то понимаю, а так нет!
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад