Question

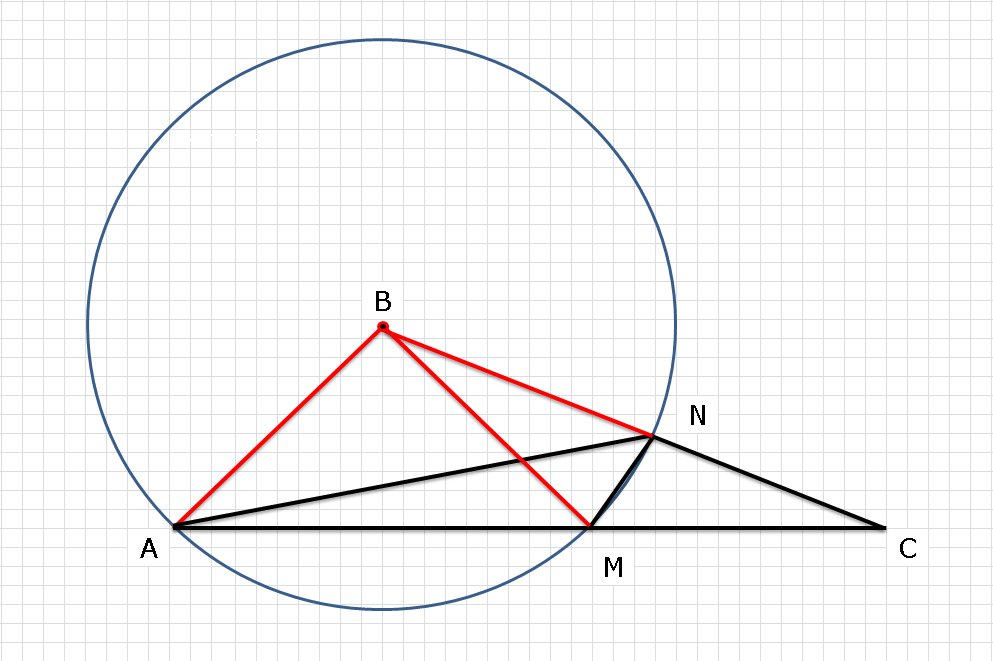
в  реугольнике авс угол а=32 градуса, угол с=24 градуса. окружность с центром в точке в проходит через вершину а и сторону ас пересекается в точке м, а сторона вс в точеке n.

найдите угол  аnм.

Answer 1

У каждого из треугольников ABM, ABN, MBN две стороны – это радиусы окружности. Значит, все эти треугольники равнобедренные.
Решаем:
< ABC = 180⁰ - (<BAC + <BCA) = 180⁰ - (32⁰+24⁰) = 124⁰    
< BMA = <BAM = 32⁰    
< ABM = 180⁰ - (<BMA + <BAM) = 180⁰ - (32⁰+32⁰) = 116⁰    
< MBN = <ABC - <ABM = 124⁰ - 116⁰ = 8⁰    
< BNM = <BMN = (180⁰ - 8⁰)/2 = 86⁰    
< BNA = <BAN = (180⁰ - 124⁰)/2 = 28⁰    
< ANM = <BNM - <BNA = 86⁰ - 28⁰ = 58⁰    
Ответ: < ANM = 58⁰