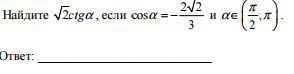Ответы
Ответ дал:
0
1. Сначала найдём синус этого угла по основному тригонометрическому тождеству:

Так как угол альфа находится во второй четверти, то sin α=1/3.
2. Найдём котангенс, умноженный на корень из двух:

Мы воспользовались тем, что котангенс -- это косинус делённый на синус.
Так как угол альфа находится во второй четверти, то sin α=1/3.
2. Найдём котангенс, умноженный на корень из двух:
Мы воспользовались тем, что котангенс -- это косинус делённый на синус.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад