Question

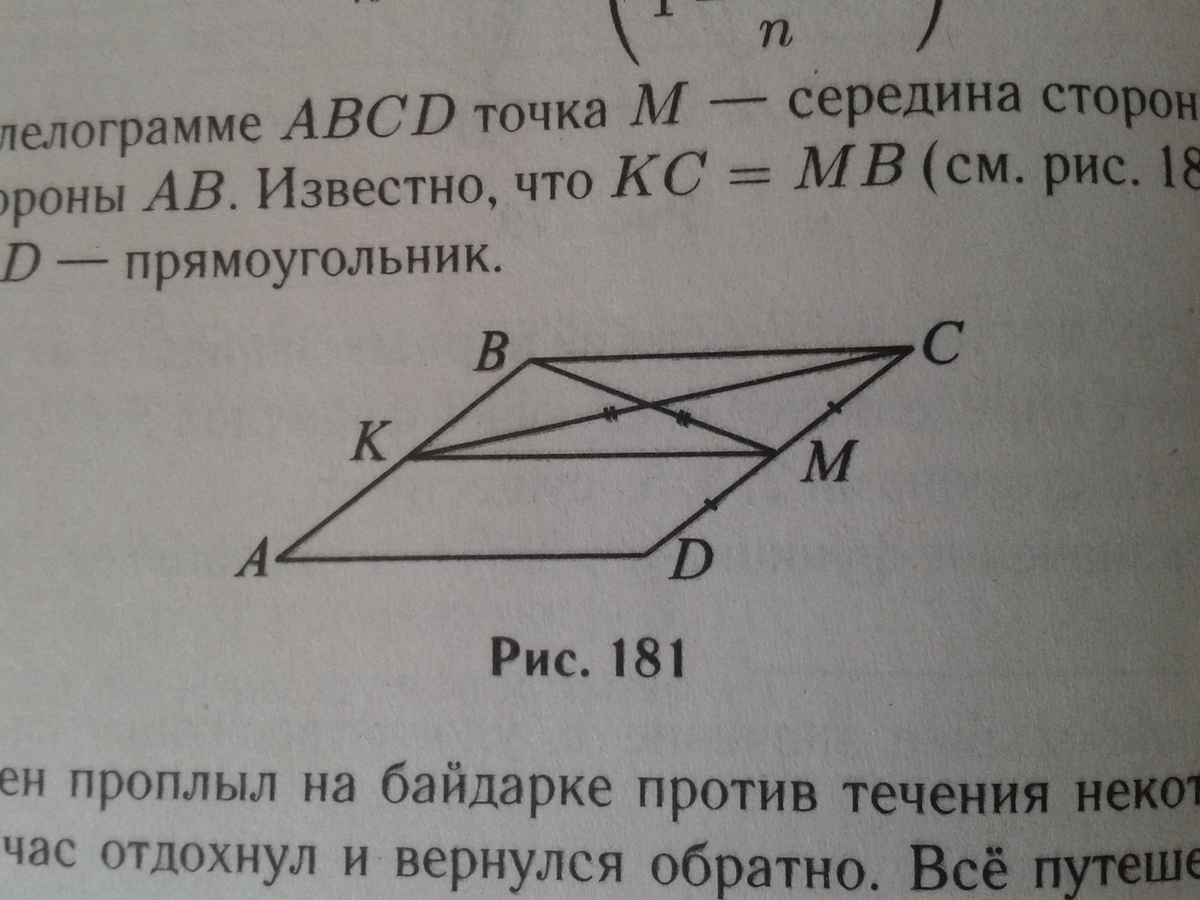
В параллелограмме ABCD точка M - середина стороны CD, K - середина стороны AB. Известно, что KC=MB. Докажите, что ABCD - прямоуглльник.

Answer 1

Треугольники КВМ и КСМ равны по трём сторонам. КС=МВ,  КМ - общая, КВ=СМ, т.к. точки К и М - середины противолежащих сторон параллелограмма. А против равных сторон в равных треугольниках лежат равные углы. Против стороны МВ лежит угол К, а протв стороны КС лежит угол М. Значит, углы К и М равны.  Они также  являютя односторонними при параллельных АВ и СД и секущей КМ. Их сумма равна 180. А если сумма равных углов равна 180, то углы равны по 90. Значит и углы А и Д, углы В и С равны по 90. АВСД - прямоугольник.