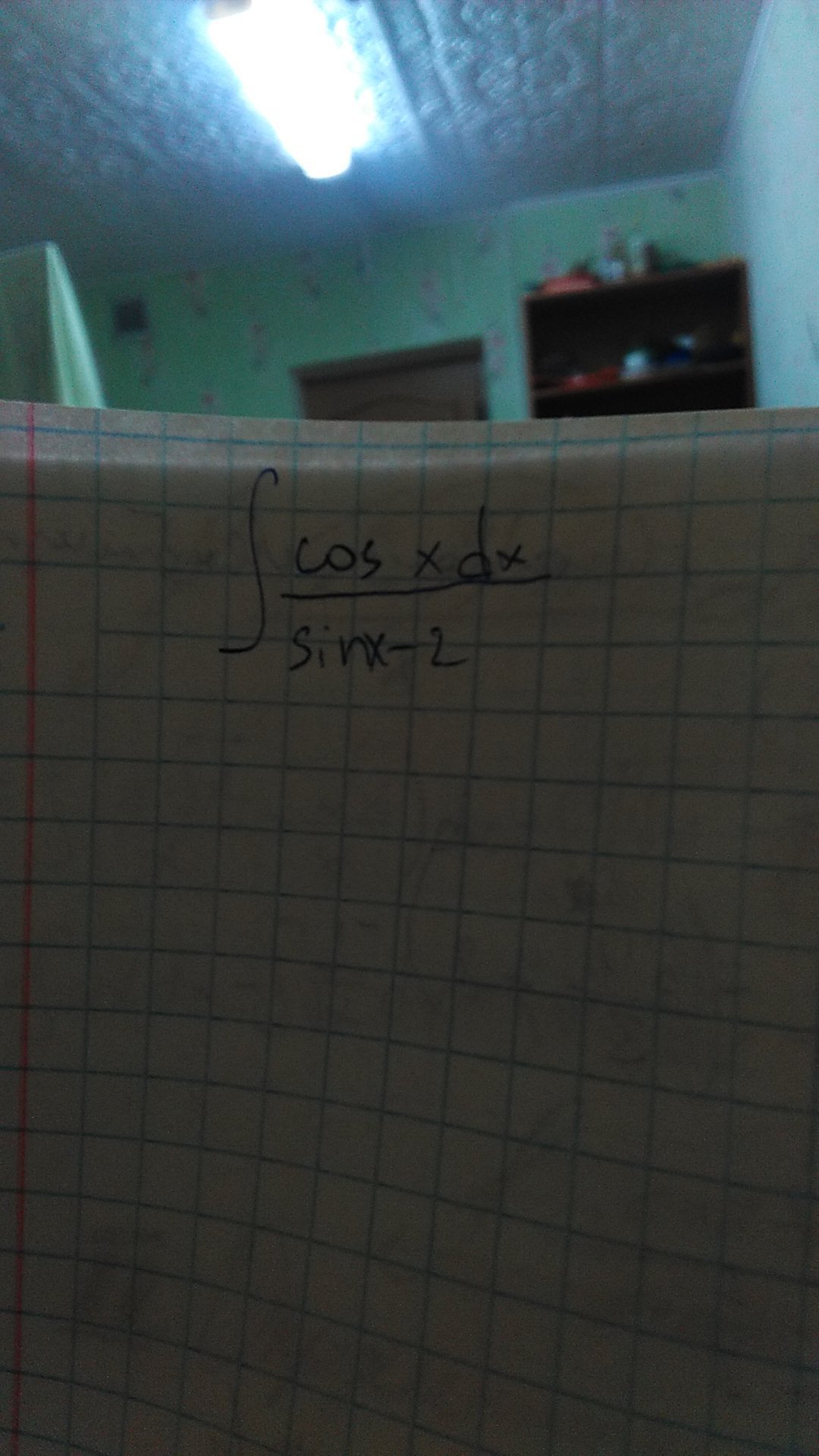Ответы
Ответ дал:
0
∫(cosxdx/(sinx-2)
Решение:
Данный интеграл вычисляется элементарно методом замены переменной.
Пусть sinx-2=t, тогда dt= cosxdx и мы получаем:
∫(cosxdx/(sinx-2)=∫ dt /t=Lnt+C
Делая обратную замену, получаем:
∫(cosxdx/(sinx-2)= Ln(sinx-2) +C
Решение:
Данный интеграл вычисляется элементарно методом замены переменной.
Пусть sinx-2=t, тогда dt= cosxdx и мы получаем:
∫(cosxdx/(sinx-2)=∫ dt /t=Lnt+C
Делая обратную замену, получаем:
∫(cosxdx/(sinx-2)= Ln(sinx-2) +C
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад