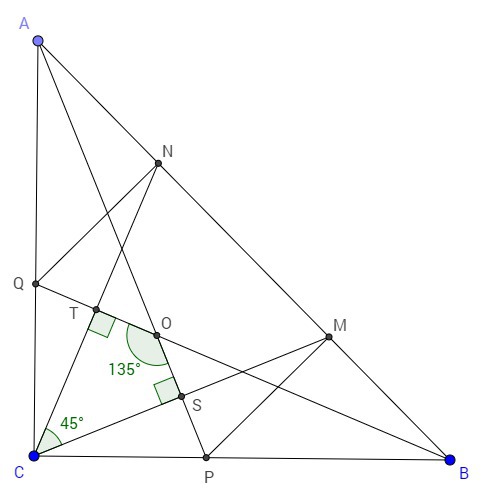
В треугольнике ABC угол C прямой. P и Q — основания биссектрис углов BAC и ABC соответственно. M — основание высоты, опущенной из точки P на гипотенузу, N — из точки Q. Найдите угол NCM . Ответ дайте в градусах, указывая только число.
Ответы
Ответ дал:
0
△ACP=△PMA
(AP-общая; ∠PAC=∠MAP; ∠ACP=∠PMA=90°)
AC=AM; △ACM равнобедренный; AS является биссектрисой и высотой; ∠ASC=90°
Аналогично △CBN равнобедренный; BT является биссектрисой и высотой; ∠BTC=90°
Угол между биссектрисами острых углов прямоугольного треугольника равен 45° (смежный 135°)
∠SOT =135°
Сумма углов четырехугольника равна 360°
Рассмотрим четырехугольник СSOT:
∠TCS + ∠CSO + ∠SOT + ∠OTC = 360°
∠TCS + 90° + 135° + 90° = 360° <=> ∠TCS = 45°
(AP-общая; ∠PAC=∠MAP; ∠ACP=∠PMA=90°)
AC=AM; △ACM равнобедренный; AS является биссектрисой и высотой; ∠ASC=90°
Аналогично △CBN равнобедренный; BT является биссектрисой и высотой; ∠BTC=90°
Угол между биссектрисами острых углов прямоугольного треугольника равен 45° (смежный 135°)
∠SOT =135°
Сумма углов четырехугольника равна 360°
Рассмотрим четырехугольник СSOT:
∠TCS + ∠CSO + ∠SOT + ∠OTC = 360°
∠TCS + 90° + 135° + 90° = 360° <=> ∠TCS = 45°
Приложения:
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад
10 лет назад