Question

дано:треугольник ABC,треугольник DCE,угол А=44 градуса,угол Е=46 градусов,угол B=90 градусов,угол D=90 градусов. доказать:BC перпендикулярно CD

Answer 1

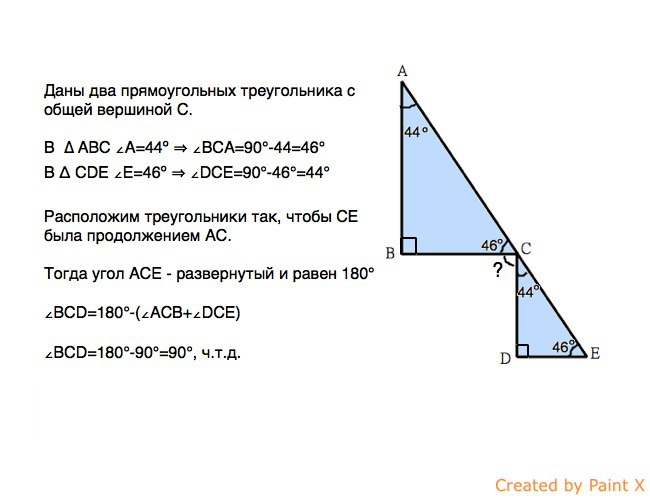
Даны два прямоугольных треугольника с общей вершиной С. 
В  ∆ АВС ∠А=44º ⇒ ∠ВСА=90°-44=46°
В Δ CDE ∠E=46º ⇒ ∠DCE=90°-46°=44°
Расположим треугольники так, чтобы СЕ была продолжением АС. 
Тогда угол АСЕ - развернутый и равен 180°
∠ВСD=180°-(∠ACB+∠DCE)
∠BCD=180°-90°=90°, а это величина угла, образованного перпендикулярными прямыми,  ч.т.д.