Точка М – середина стороны АВ параллелограмма ABCD. Докажите, что площадь
треугольника МВС составляет ¼ площади параллелограмма.
Помогите пожалуйста))..
Ответы
Ответ дал:
0
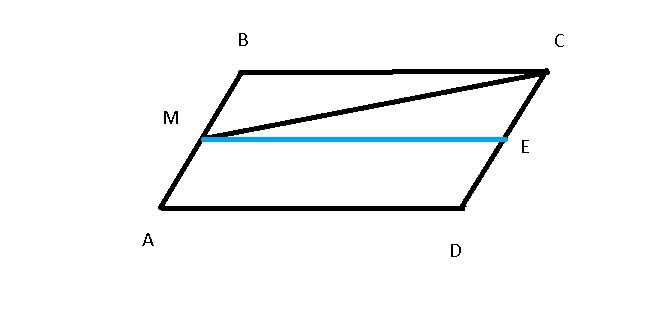
Через точку М проведем прямую АЕ параллельную AD
так как М - середина то прямая АЕ разделит параллелограмм на 2 равные фигуры каждая из которых параллелограмм
SMBCE=(1/2)SABCD
так как МС диагональ параллелограмма МВСЕ то она делит его на 2 равных треугольника ⇒ SMBC=SMCE
SMBC=(1/2)SMBCE=(1/2)((1/2)ABCD)=1/4(ABCD)
так как М - середина то прямая АЕ разделит параллелограмм на 2 равные фигуры каждая из которых параллелограмм
SMBCE=(1/2)SABCD
так как МС диагональ параллелограмма МВСЕ то она делит его на 2 равных треугольника ⇒ SMBC=SMCE
SMBC=(1/2)SMBCE=(1/2)((1/2)ABCD)=1/4(ABCD)
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад