Question

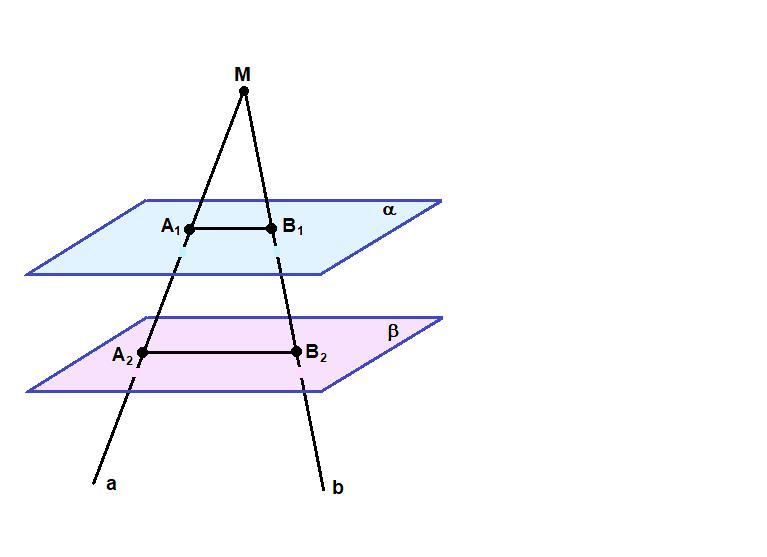
Через точку M, не лежащую между параллельными плоскостями α и β, проведены прямые a и

b. Прямая a пересекает плоскости α и β в точках А1 и А2 соответственно, прямая b – в точках В1

и В2. Найдите длину отрезка А2В2, если А1В1= 15 см, ОВ1 : ОВ2 = 3 : 5. и рисунок

Answer 1

Ответ:   25 см

Условие задачи:

Через точку M, не лежащую между параллельными плоскостями α и β, проведены прямые a и  b. Прямая a пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая b – в точках В₁ и В₂.

Найдите длину отрезка А₂В₂, если А₁В₁ = 15 см, МВ₁ : МВ₂ = 3 : 5.

Пошаговое объяснение:

Пересекающиеся прямые а и b лежат в одной плоскости, которая пересекает параллельные плоскости α и β по прямым А₁В₁ и А₂В₂. Значит

А₁В₁ ║ А₂В₂.

∠МА₁В₁ = ∠МА₂В₂ как соответственные при пересечении параллельных прямых А₁В₁ и А₂В₂ секущей а,

∠М - общий для треугольников МА₁В₁ и МА₂В₂, значит

Δ МА₁В₁ подобен  ΔМА₂В₂ по двум углам.

A₁B₁ : A₂B₂ =  МВ₁ : МВ₂ = 3 : 5

15 : A₂B₂ = 3 : 5

A₂B₂ = 15 · 5 / 3 = 25 см