Question

постройте график функции y=2x^2+4x-6

Answer 1

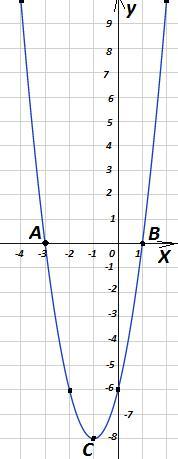
y = 2x² + 4x - 6 ;      a = 2;  b = 4;  c = -6

Функция квадратичная, график - парабола, ветви направлены вверх (а=2>0).  График пересекает ось OY в точке (0; -6), так как с=-6.

Координаты вершины параболы :

$x_0=-dfrac b{2a}=-dfrac4{2cdot 2}=-1;\\y_0=2cdot (-1)^2+4cdot (-1)-6=2-4-6=-8$

Дополнительные точки для построения :

x  |    -4    -3    -2    1    2

y  |   10     0    -6    0   10

a) Нули функции  x₁ = -3;  x₂ = 1   (точки A  и  В)

б) y < 0  при  x ∈ (-3; 1)

   y > 0  при  x ∈ (-∞; -3)∪(1; +∞)

в) x ∈ (-∞; -1]     - функция убывает

   x ∈ [-1; +∞)     - функция возрастает

г) наименьшее значение функции в вершине  y₀ = -8

д) E (y) = [-8; +∞)   - область значений функции