радиус окружности, описанной около правильного многоугольника равен 2√3 см, а радиус окружности, вписанной в него - 3 см. Найдите: 1) сторону многоугольника, 2) количество сторон многоугольника.
Ответы
Описанный :R
Вписанный :r
Сторона :а
а^2/4=R^2-r^2=12-9=3
a^2=12
a=2(3^1/2)
Отсюда видно что a=R. Значит количество сторон n(a)=6
Ответ: 1) 2√3 см; 2)6 сторон
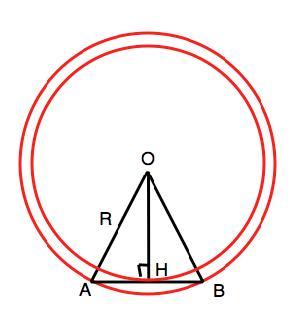
Объяснение: Центр окружности, вписанной в правильный n-угольник. совпадает с центром окружности, описанной около него. Такой многоугольник по числу сторон можно разделить на n равных равнобедренных треугольников с вершиной в центре окружностей. Боковыми сторонами каждого такого треугольника будут радиусы описанной окружности, высотой - радиус вписанной окружности.
Пусть центр окружностей О, АО=ВО=R=2√3; ОН=r=3 =⇒
sin ∠OAH=OH:OA=3:2√3== это синус угла 60°. Треугольник АОВ равнобедренный ⇒ угол АОВ=60°⇒ ∆АОВ - равносторонний, АВ=АО=R=2√3,.
Градусная величина полного угла 360°. Следовательно, n=360:60=6 (сторон многоугольника)