Question

Геометрия 8 класс. Гимназическая программа, которую не тянут и в 11...
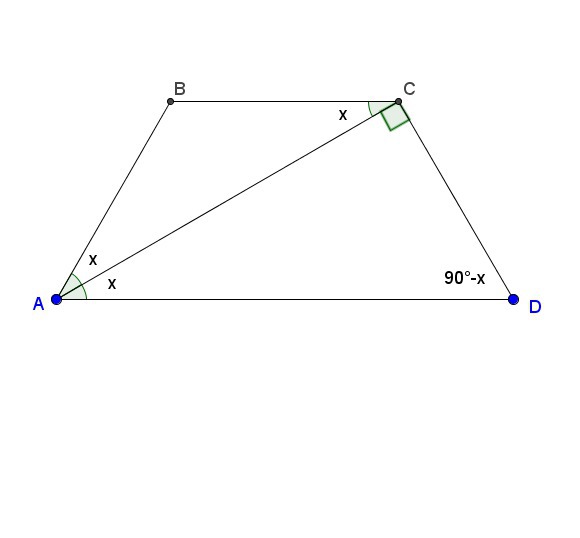
Равнобедренная трапеция ABCD. AC - диагональ. AC перпендикулярно CD. Основание BC равно сторонам AB и CD. Найти углы A и В.

Answer 1

Пусть ∠CAD=х.
∠ACB=∠CAD=x как внутренние накрест лежащие при параллельных прямых BC и AD.
 ∠BAC=∠ACB=x как углы при основании равнобедренного треугольника ABC (в нем AB=BC).
∠BAD=∠ADC=90°-∠CAD=90°-x (т.к.∠ACD=90° и трапеция равнобедренная).
Итак, ∠BAD=∠BAC+∠CAD=2x=90°-x, откуда 3х=90°, т.е. х=30°, а значит ∠A=2*30°=60°, ∠B=180°-60°=120°.

Answer 2

Добавил чертежик