Привести уравнение кривой второго порядка x^2 + 4y^2 + 4x - 8y - 8 = 0 к каноническому виду. Определить тип кривой, её параметры и сделть рисунок
Ответы
Ответ дал:
0
Выделяем полные квадраты:
(x+2)² -4 +4*(y-1)² - 4 -8 =0
(x+2)² + 4*(y-1)² = 16
Разделим обе части уравнения на 16:
(x+2)² / 4² + (y-1)² / 2² = 1
Получили уравнение ЭЛЛИПСА
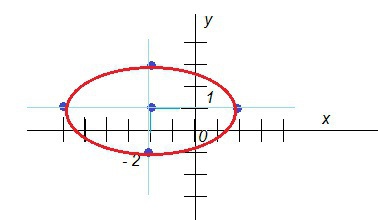
Центр эллипса (-2; 1)
Полуоси:
a=4; b=2
Чертим рисунок:(См скрин)
(x+2)² -4 +4*(y-1)² - 4 -8 =0
(x+2)² + 4*(y-1)² = 16
Разделим обе части уравнения на 16:
(x+2)² / 4² + (y-1)² / 2² = 1
Получили уравнение ЭЛЛИПСА
Центр эллипса (-2; 1)
Полуоси:
a=4; b=2
Чертим рисунок:(См скрин)
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад