Ребро куба ABCDA1B1C1D1 равно a. Постройте сечение куба , проходящее через середины ребер А1В1, СС1, АД и найдите площадь этого сечения.
Ответы
Ответ дал:
24
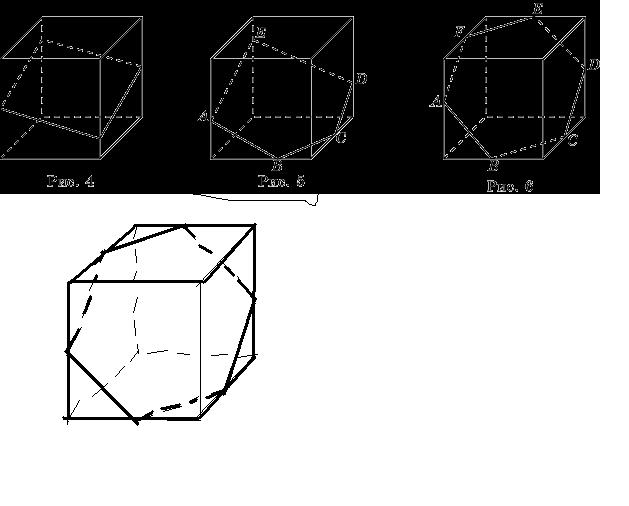
На рисунке 6 показано сечение куба плоскостью в форме шестиугольника ABCDEF. Прямые AB и DE, BC и EF, CD и AF параллельны, как линии пересечения двух параллельных плоскостей третьей плоскостью.
Таким образом, в сечении куба плоскостью может получиться только тот шестиугольник, у которого имеется три пары параллельных сторон.
Так как исходные точки - это середины ребер, то в сечении получается правильный шестиугольник. Обозначим его сторону за "b". b = V((a/2)^2 + (a/2)^2) = (a/2) * V2 = a / V2.
S = 3/2*V3*b^2 = 3/2*V3*(a / V2)^2 = 3V3*a^2 / 4.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад