катеты прямоугольного треугольника равны 12 см и 16 см. Найдите длину биссектрисы треугольника, проведенную из вершины большего острого угла.
Ответы
Ответ дал:
0
Ответ: 6√5 см
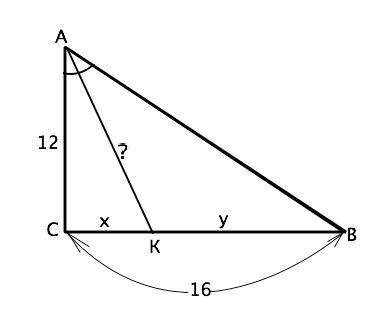
Пусть в треугольнике АВС угол С=90°, АС=12 см, СВ=16 см, АК - биссектриса.
Решение:
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
Примем длину СК=х, ВК=у. Тогда х:у=АС:АВ.
По т.Пифагора АВ=√(АС²+ВС²)=√(144+256)=20 ⇒
х:у=12:20=3/5 Следовательно, ВС состоит из х+у=3+5=8 частей. Длина каждой части 16:8=2 см. ⇒ СК=2•3=6 см
Из прямоугольного ∆ АСК по т.Пифагора АК=√(AC²+CK²)=√(144+36)=√180=6√5 см
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад