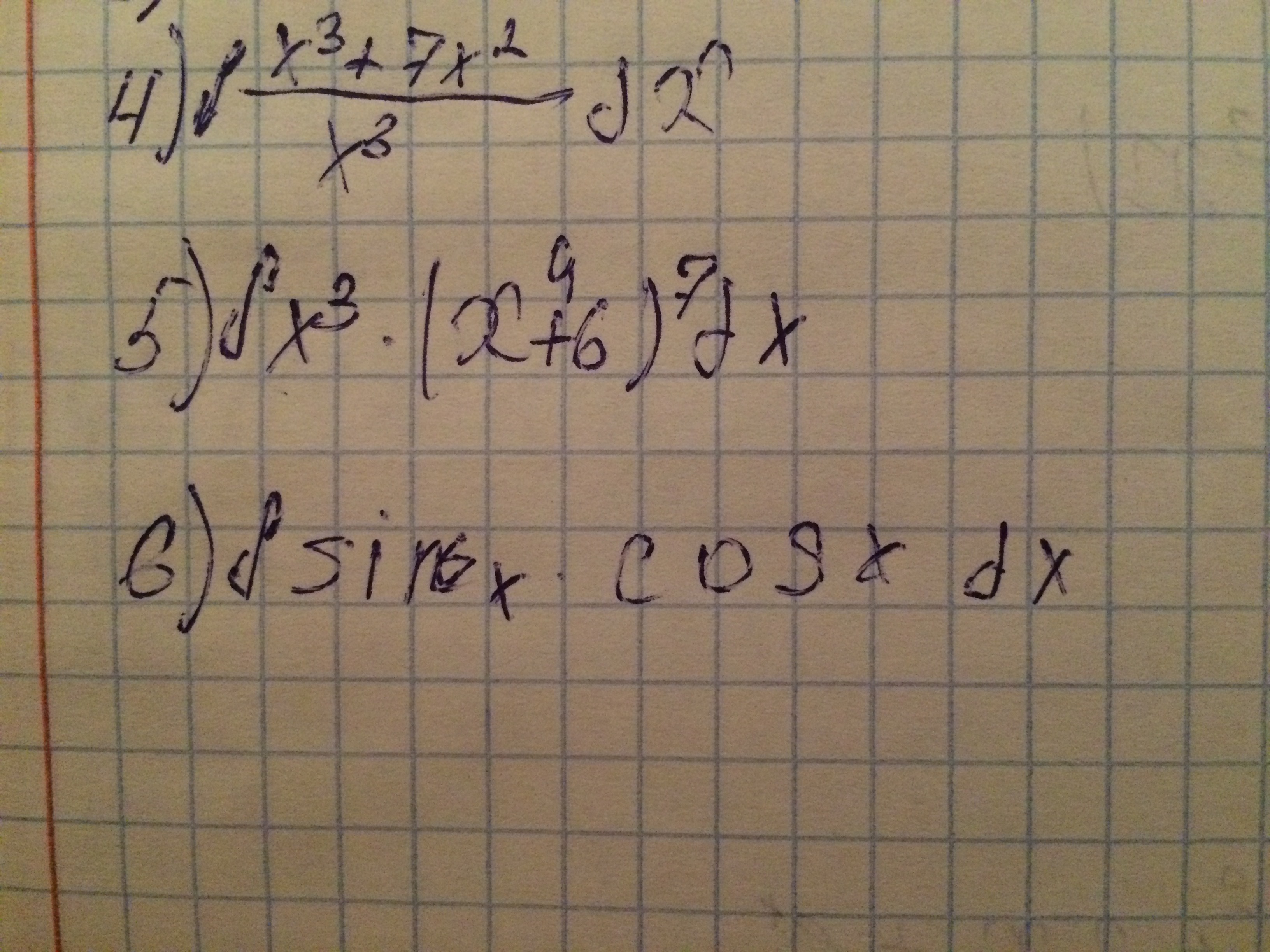Ответы
Ответ дал:
0
4) Преобразуем подынтегральное выражение (представим в виде суммы двух слагаемых) 
Найдем интеграл от суммы

5) пусть t= Умножаем подынтегральное выражение на произведение 14 и 4, выносим 14 за знак интеграла получаем
Умножаем подынтегральное выражение на произведение 14 и 4, выносим 14 за знак интеграла получаем 
6) Метод подстановки. t = sinx, cosx = , dx=
, dx=
После замены в подынтегральном выражении получаем
Найдем интеграл от суммы
5) пусть t=
6) Метод подстановки. t = sinx, cosx =
После замены в подынтегральном выражении получаем
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад