Question

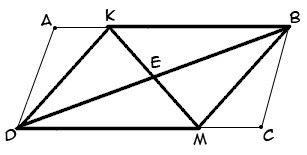
"Прямая пересекает диагональ ВD параллелограмма АВСD в точке Е, а его стороны АВ и СD - в точках М и К в соответствии, причем МЕ = КЕ. Докажите, что четырехугольник ВКDМ - параллелограмм."
Буду очень благодарен, если кто поможет.
(попытался составить рисунок)

Answer 1

ME=KE (по условию), BE=ED(по свойствам параллелограмма ABCD). Значит, диагонали BKDM точкой пересечения делятся пополам следовательно BKDM- параллелограмм (по признаку параллелограмма). Чертеж правильный.

Answer 2

Большое спасибо!