Помогите пожалуйста с алгеброй!!!
Доказать ,что функция f(x) была непрерывна в точке а ,если :
Приложения:
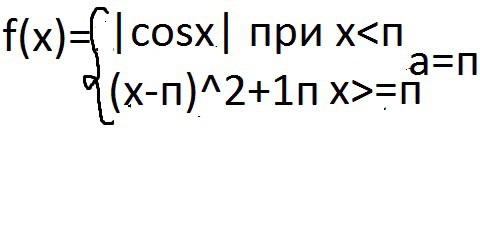
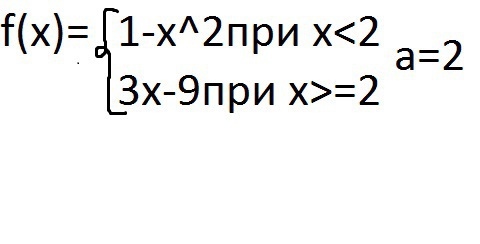
Ответы
Ответ дал:
0
f(π-0)=|cosπ|=|-1|=1
f(π+0)=(π-π)²+1=1
f(π)=(π-π)²+1=1
Функция является непрерывной в точке х=π, предел функции слева равен пределу функции справа, равен значению функции в точке
f(2-0)=1-(2-0)²=-3
f(2+0)=3·2-9=-3
f(2)=3·2-9=-3
Функция является непрерывной в точке х=2, предел функции слева равен пределу функции справа, равен значению функции в точке.
f(π+0)=(π-π)²+1=1
f(π)=(π-π)²+1=1
Функция является непрерывной в точке х=π, предел функции слева равен пределу функции справа, равен значению функции в точке
f(2-0)=1-(2-0)²=-3
f(2+0)=3·2-9=-3
f(2)=3·2-9=-3
Функция является непрерывной в точке х=2, предел функции слева равен пределу функции справа, равен значению функции в точке.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад