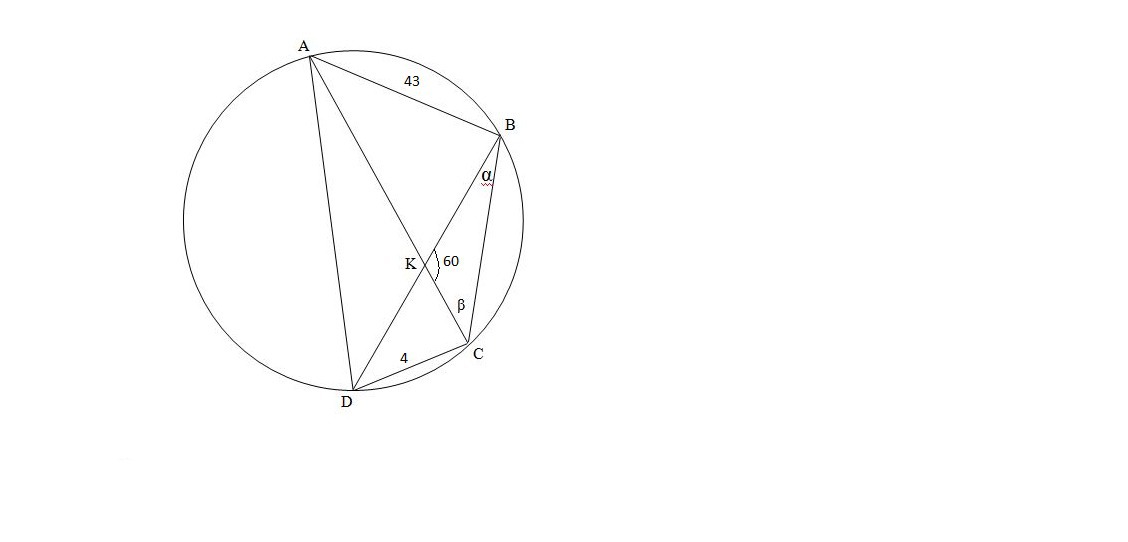
Вокруг выпуклого четырёхугольника ABCD описана окружность. К - точка пересечения диагоналей данного четырёхугольника. Угол ВKС = 60 градусов, АВ = 43, DС = 4. Найти радиус описанной окружности.
Ответы
Ответ дал:
0
∠
Воспользуемся:
Для произвольного треугольника ABC выполняется равенство
Пусть ∠
Рассмотрим Δ
Δ
Δ
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад