Ответы
Ответ дал:
0
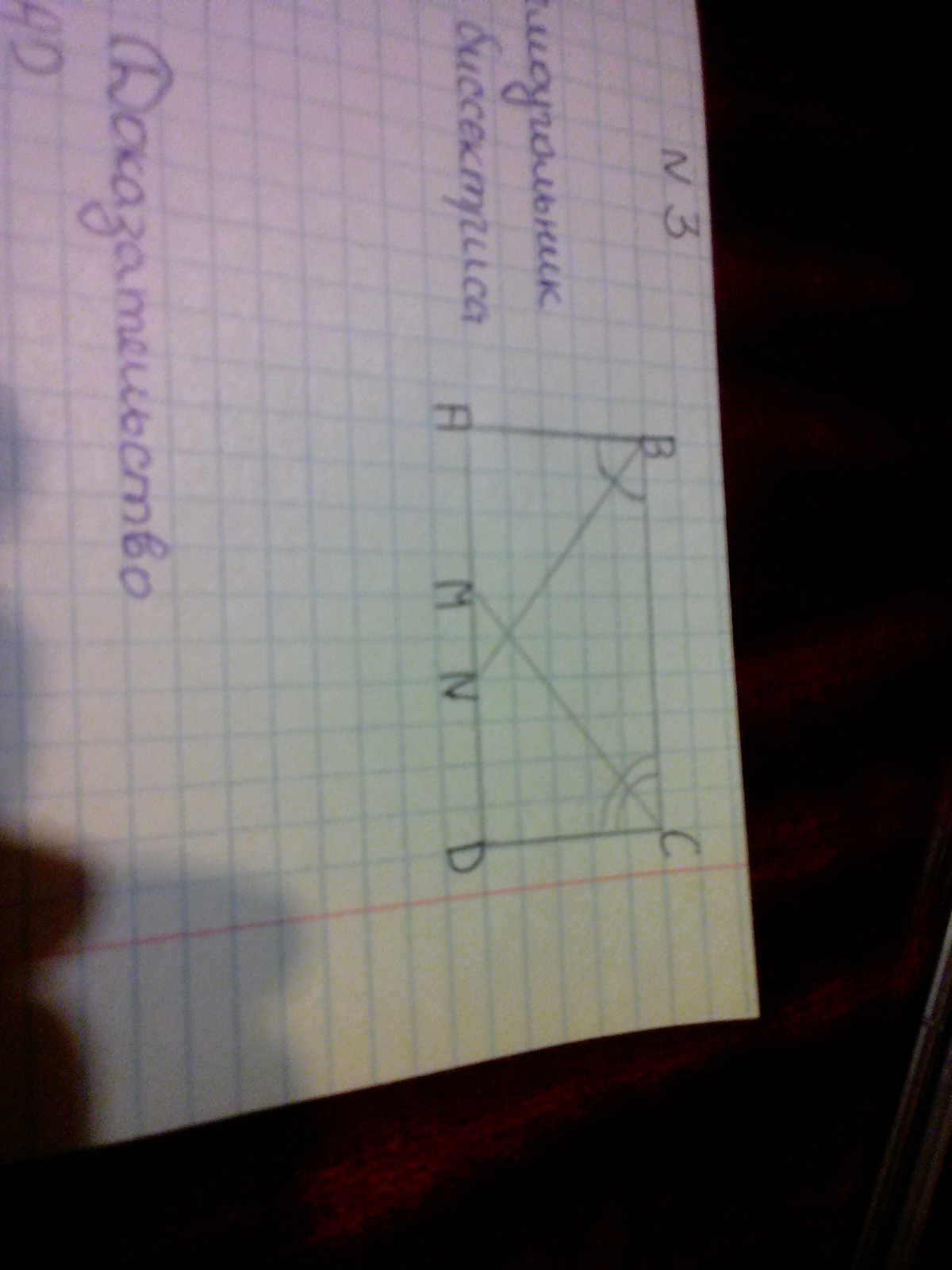
Дано: ABCD - прямоугольник, СМ, BN - биссектрисы ∠С и ∠В. Доказать: АМ = ND
===========================================================
CM - биссектриса ∠С ⇒ ∠МCD = ∠BCM = ∠C/2 = 90°/2 = 45°
BN - биссектриса ∠В ⇒ ∠ABN = ∠CBN = ∠B/2 = 90°/2 = 45°
ΔABN = ΔCDM по катету и острому углу (АВ = CD, ∠ABN = ∠MCD) ⇒ AN = MD
AM = AN - MN , ND = MD - MN , но AN = MD
Значит, AM = ND, что и требовалось доказать.
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад