Ответы
Ответ дал:
0
Соединим точки С и М.
Точка М - середина основания АD, поэтому АМ=МD. Значит АМ=ВС и
четырехугольник АВСМ - параллелограмм по признаку:
"Если в четырехугольнике две стороны равны и параллельны, то этот
четырехугольник будет являться параллелограммом".
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°, а противоположные углы равны.
Следовательно, Ответ:
Точка М - середина основания АD, поэтому АМ=МD. Значит АМ=ВС и
четырехугольник АВСМ - параллелограмм по признаку:
"Если в четырехугольнике две стороны равны и параллельны, то этот
четырехугольник будет являться параллелограммом".
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°, а противоположные углы равны.
Следовательно, Ответ:
Ответ дал:
0
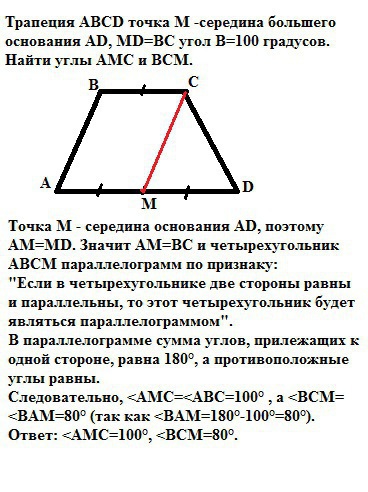
Соединим точки С и М.
Точка М - середина основания АD, поэтому АМ=МD. Значит АМ=ВС и
четырехугольник АВСМ - параллелограмм по признаку:
"Если в четырехугольнике две стороны равны и параллельны, то этот
четырехугольник будет являться параллелограммом".
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°, а противоположные углы равны.
Следовательно, <AMC=<АВС=100° , а <ВСМ=<BAМ=80° (так как <BAМ=180°-100°=80°).
Ответ: <AMC=100°, <ВСМ=80°.
Точка М - середина основания АD, поэтому АМ=МD. Значит АМ=ВС и
четырехугольник АВСМ - параллелограмм по признаку:
"Если в четырехугольнике две стороны равны и параллельны, то этот
четырехугольник будет являться параллелограммом".
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°, а противоположные углы равны.
Следовательно, <AMC=<АВС=100° , а <ВСМ=<BAМ=80° (так как <BAМ=180°-100°=80°).
Ответ: <AMC=100°, <ВСМ=80°.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад