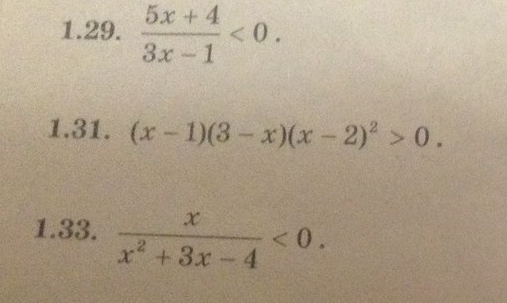Ответы
Ответ дал:
8
Рациональная функция будет принимать отрицательные значения, когда знаки числителя и знаменателя будут различны. Решим методом интервалов:
-------------- () +++++++++
-------------- () +++++++++
++++++ ()--------(
) ++++++
Решаем методом интервалов. Знак функции, когда x проходит через корень четной кратности - не изменяется. Смотрим на знак функции при x большем наибольшего из корней и меняем знак всякий раз, когда проходим через корень нечетной кратности.
------------- 1 +++++++ 2 +++++++ 3 -------------
Выбрасываем x = 2, так как в этой точке функция обращается в ноль.
Решаем методом интервалов:
------------------ 0 +++++++++++
+++++++ (-4) ---------- 1 +++++++
------- (-4) +++++ 0 ------- 1 +++++++
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад