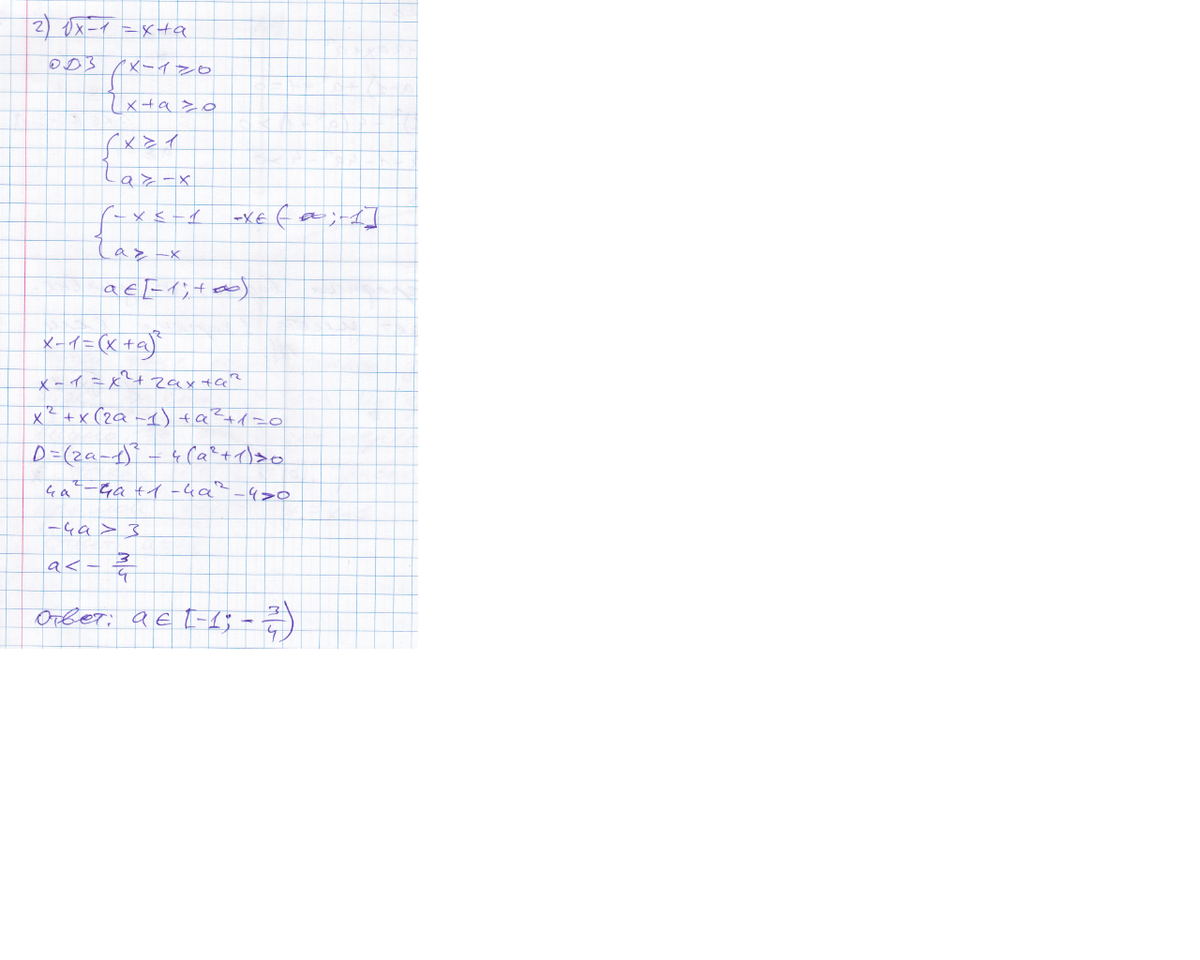Question

УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРАМИ.

Так мне поможет кто-нибудь!? Кто не знает не суйтесь! Если решение окажется не полным отмечаю как нарушение!!!

 

№1. При каких значениях  $a$  параметра уравнение  $|x^2-6x-5|=a$  имеет не менее трёх корней?

 

№2. При каких значениях  $a$  уравнение имеет  $sqrt{x-1}=x+a$  два корня?

 

№3. При каком значении  $a$  один из корней уравнения  $4x^2-15x+4a^3=0$  есть квадрат другого?

 

При каком значении параметра  $a$  сумма квадратов корней уравнения  $x^2-ax+a-1=0$  равна  1$17$?

Answer 1

Во вложении

-----------------------------------------------------------------------------------

Answer 2

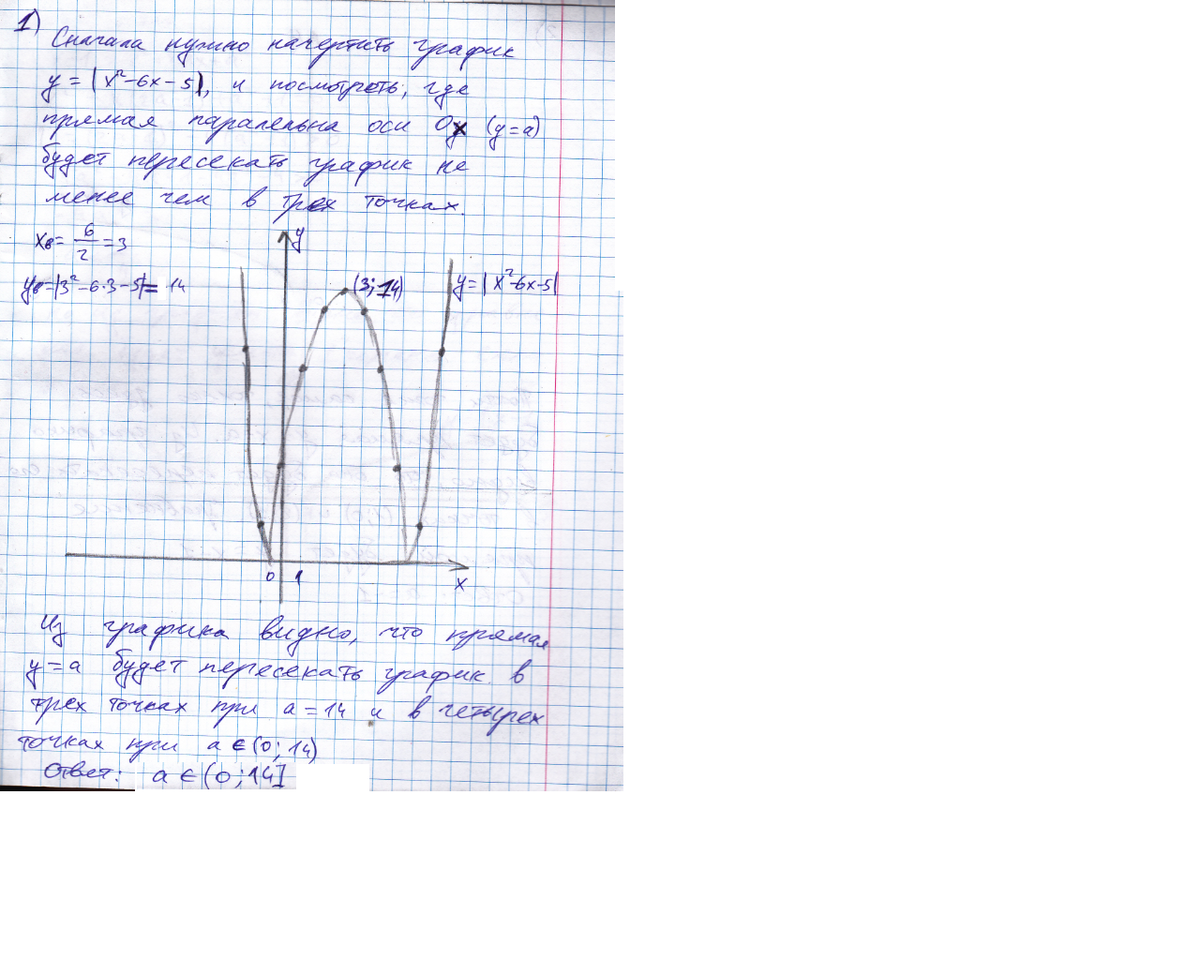
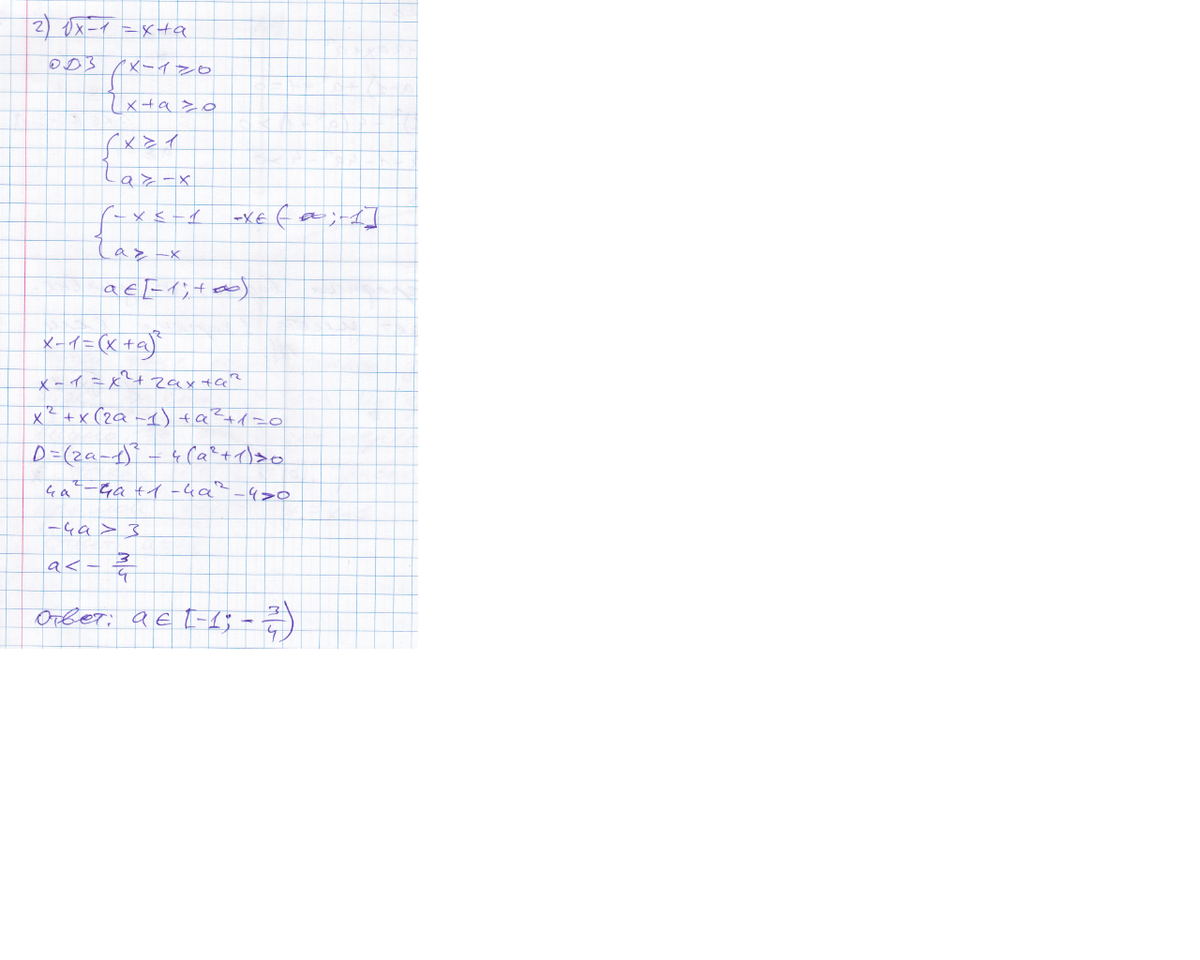
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,

а нижнее а=0.

находим вершину параболы, х0=-b/2a у нам b=6 a=-1  x0=3

y0=-9+5+18=14

значит а [0;14]

2) sqrt(x-1)=a+x  x>=1

x-1=x^2+a^2+2ax

x^2+(2a-1)x+a^2+1=0

D>0  (2a-1)^2-4a^2-4>0  -4a-3>0  a<-3/4

3) 4x^2-15x+4a^3=0

x1=x2^2

x1*x2=a^3

x2^3=a^3  x2=a

15/4=x1+x2  15/4=a^2+a

4a^2+4a-15=0  a1=3/2  a2=-5/2

x^2-ax+(a-1)=0

x1^2+x2^2=(x1+x2)^2-2x1x2=17

a^2-2(a-1)=17

a^2-2a-15=0

a1=5 a2=-3