Помогите решить!!! Используя формулы сложный корней, докажите, что значение выражения
sqrt{x+2 sqrt{x-1} }- sqrt{x-2 sqrt{x-1} }
при x geq 2 не зависит от переменной x
Приложения:
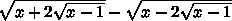
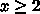
Ответы
Ответ дал:
0
при
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад