построить график функции.вычислить площадь фигуры.ограниченной осью абциссеюграфиком функции.у=х^2-3 и прямыми х=1 х=1.5
Ответы
Ответ дал:
0
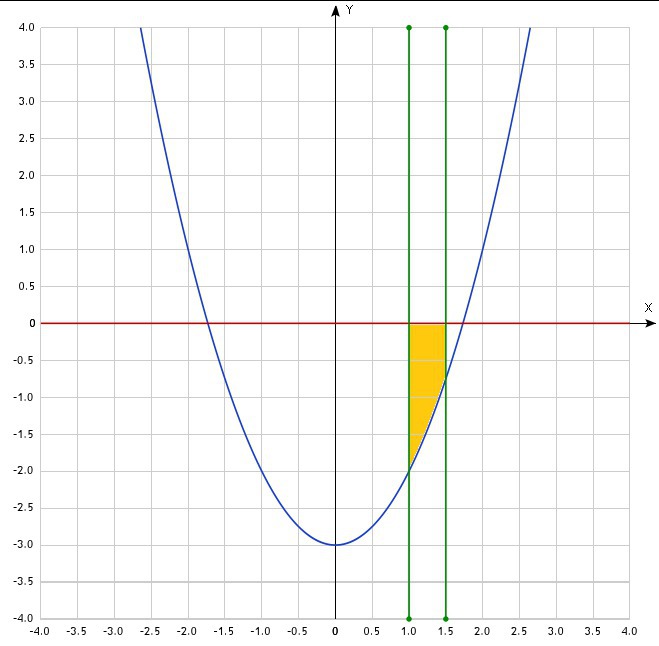
На координатной плоскости чертим график y=x²-3 это парабола ветви которой направлены вверх. Искомая фигура расположена ниже оси ОХ, значит при вычислении площади необходимо перед интегралом поставить знак минус. Пределы интегрирования определены прямыми х=1 и х=1,5. Найдём площадь:

 ед².
ед².
Приложения:
Вас заинтересует
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад