биссектриса am параллелограмма abcd делит сторону bc на отрезки bm=5 см, mc=8 см. найдите периметр параллелограмма
Ответы
Ответ дал:
0
Так как
Значит Δ
Ответ: 36 см
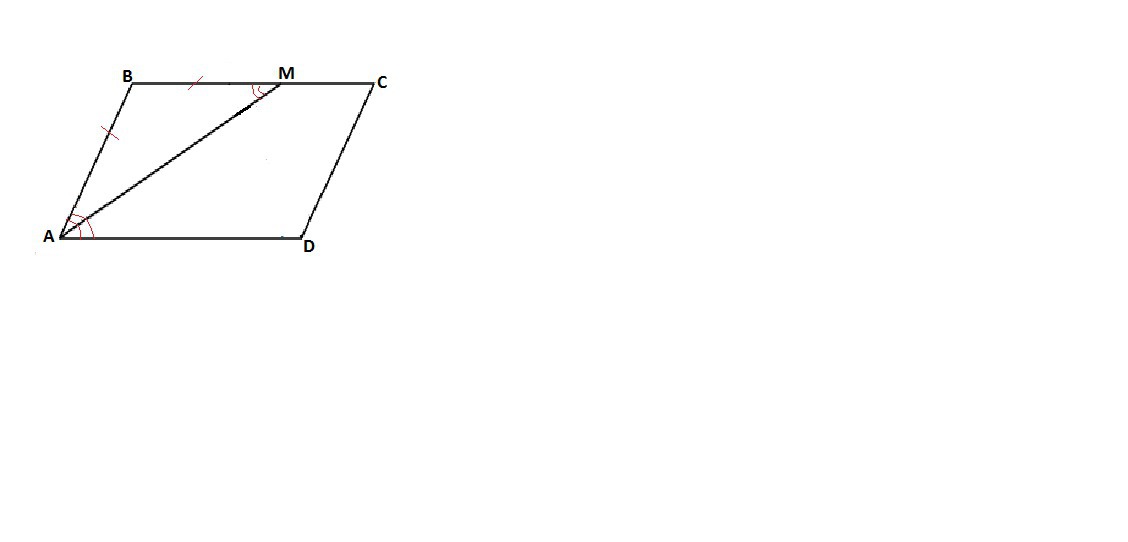
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад