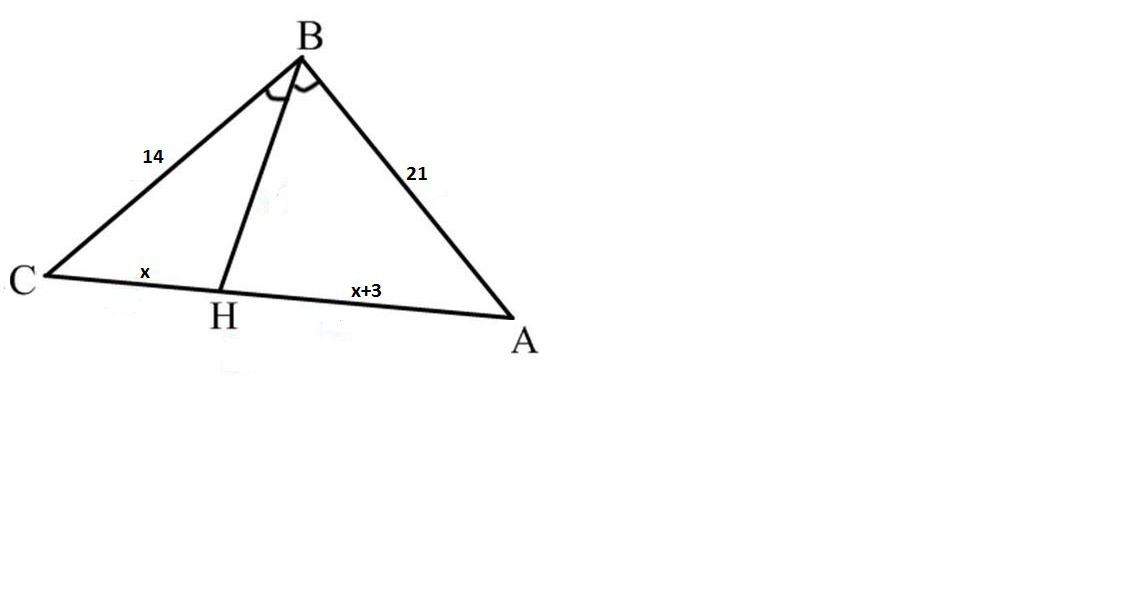
Бiсектриса трикутника дiлить його сторону на два вiдрiзки, один з яких на 3 см бiльший. Двi iншi сторони дорiвнюють 21 и 14 см.Знайдіть площу трикутника.
Ответы
Ответ дал:
0
Δ  произвольный
произвольный
 см
см
 см
см

Пусть см, тогда
см, тогда  см
см
Воспользуемся свойством биссектрисы:
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части пропорциональные сторонам:






 см
см
 см
см
 см
см
Найдём площадь треугольника с помощью формулы Герона:
 ,
, 


 см²
см²
Ответ: см²
см²
Пусть
Воспользуемся свойством биссектрисы:
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части пропорциональные сторонам:
Найдём площадь треугольника с помощью формулы Герона:
Ответ:
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад