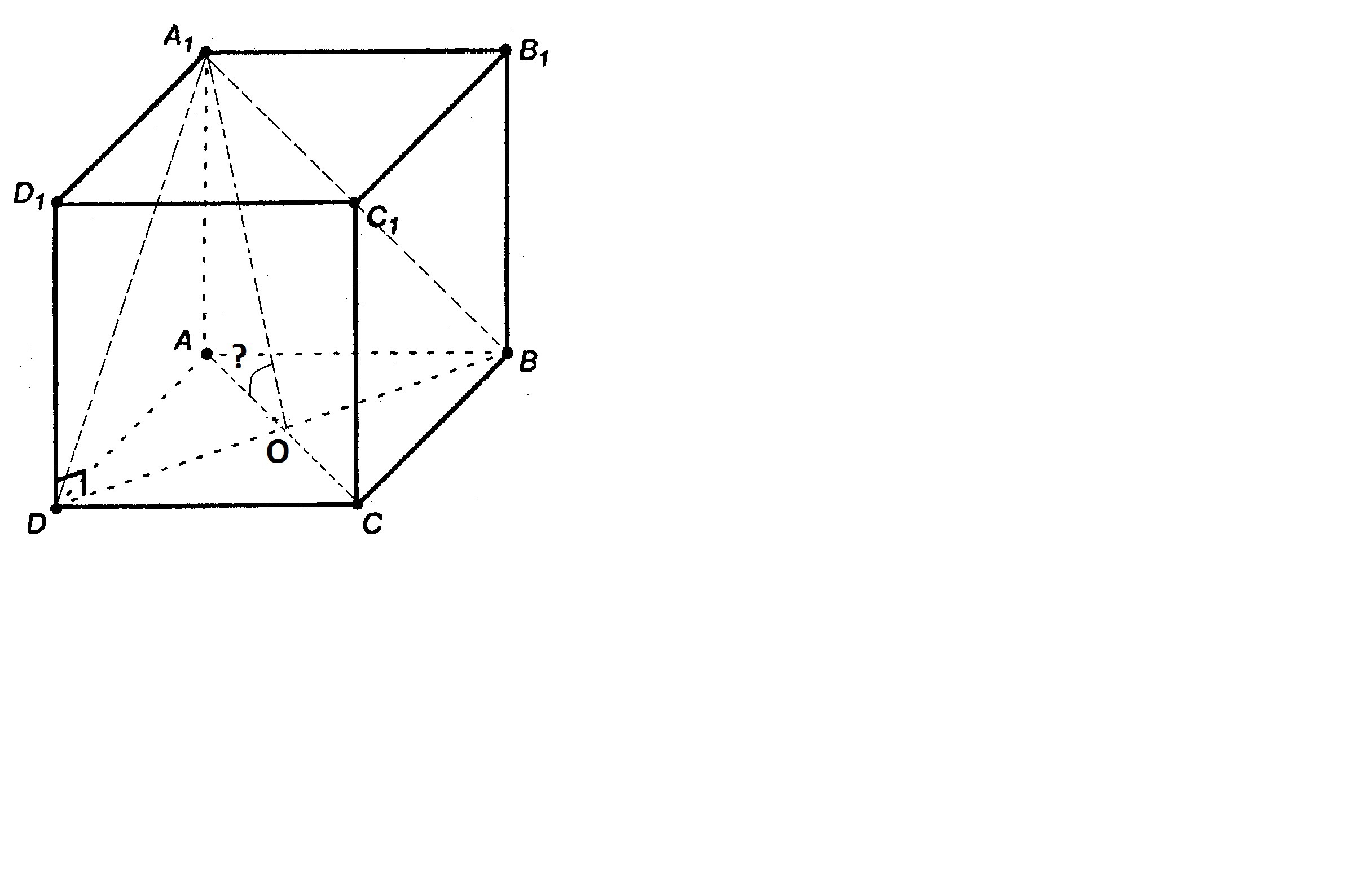
Стороны основания прямоугольного параллелепипеда ABCDA1B1C1D1 равны 8 и 6, боковое ребро равно 4,8.Найдите величину угла, образованного плоскостями ABC и A1BD.
Ответы
Ответ дал:
0
1)
 двугранный угол
двугранный угол
 линейный угол двугранного угла
линейный угол двугранного угла  , так как
, так как
 ⊥
⊥  (по теореме о 3-х перпендикулярах)
(по теореме о 3-х перпендикулярах)
 ⊥
⊥  (
(  ⊥
⊥  как диагонали прямоугольника)
как диагонали прямоугольника)
2)

 прямоугольник, значит
прямоугольник, значит 
Δ прямоугольный
прямоугольный
По теореме Пифагора:






Δ :
:



Ответ:
2)
Δ
По теореме Пифагора:
Δ
Ответ:
Приложения:
Ответ дал:
0
а сколько будет ответ в градусах просто мне тут указано а) 90 градусов
Ответ дал:
0
б) 60 градусов, в) 45 градусов и г) 30 градусов
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад