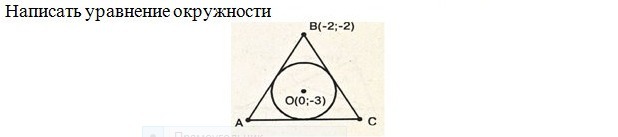
9 КЛАСС ГЕОМЕТРИЯ.Написать уравнение окружности, вписанной в треугольник ABC. Центр(0;-3) B(-2;-2)
Приложения:
Ответы
Ответ дал:
0
1. Т.к. ABC - равносторонний, центр окружности O лежит на высоте BH, проведённой к стороне AC. Поэтому радиус вписанной окружности  . Найдём
. Найдём  .
.
а) . Значит,
. Значит,  .
.
б) В равностороннем треугольнике все высоты являются медианами, которые, в свою очередь, делятся точкой пересечения в отношении , считая от вершины. Поэтому
, считая от вершины. Поэтому  . Отсюда имеем:
. Отсюда имеем:  .
.
Таким образом, нашли радиус вписанной окружности .
.
2. Составим уравнение окружности, проходящей через т. радиусом
радиусом  . Имеем:
. Имеем:



Ответ:
а)
б) В равностороннем треугольнике все высоты являются медианами, которые, в свою очередь, делятся точкой пересечения в отношении
Таким образом, нашли радиус вписанной окружности
2. Составим уравнение окружности, проходящей через т.
Ответ:
Приложения:
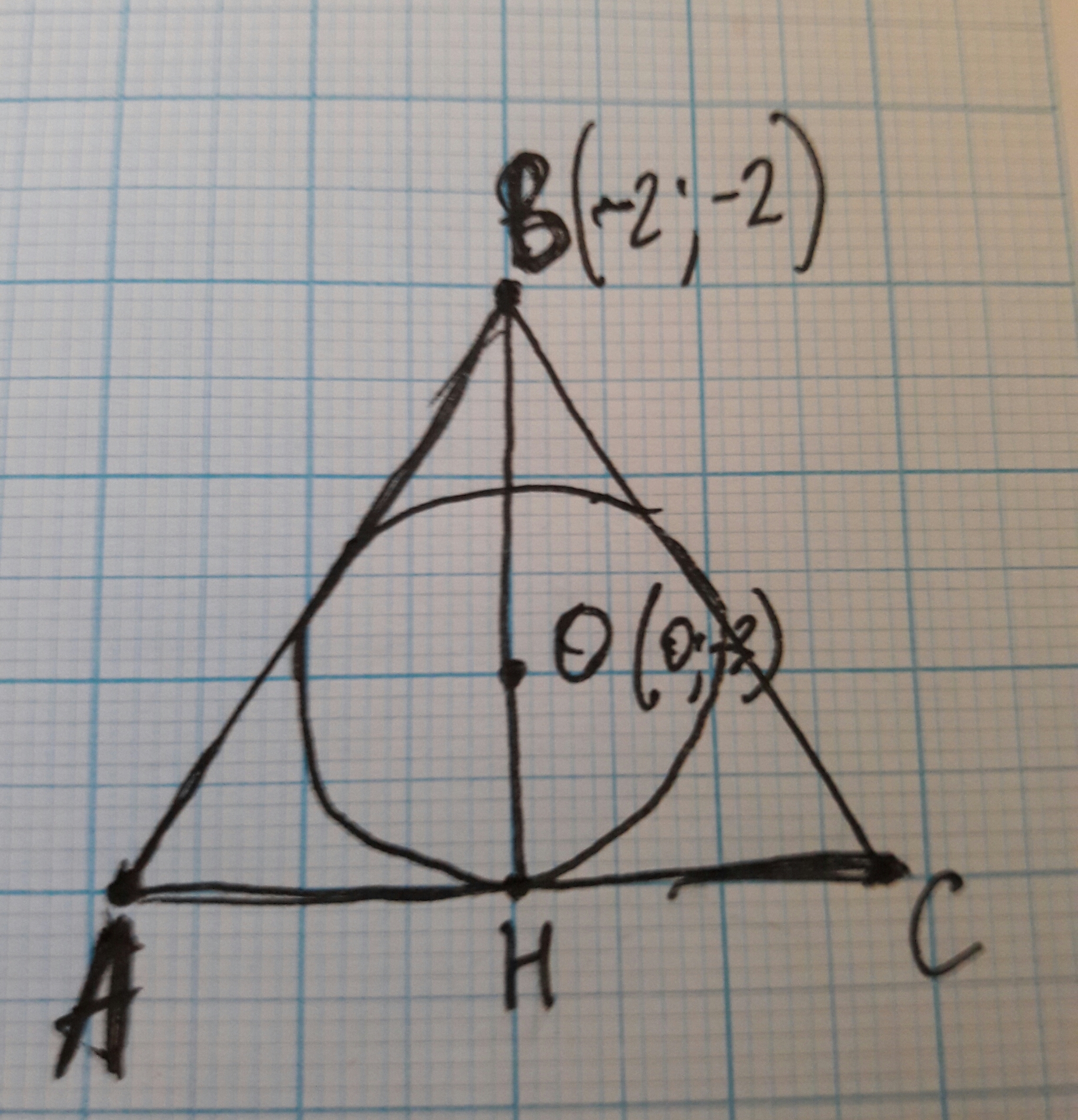
Ответ дал:
0
Благодарю
Ответ дал:
0
Пожалуйста:) Главное, чтобы поняли, как решаются геометрические задачи координатным методом.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад