Ответы
Ответ дал:
0
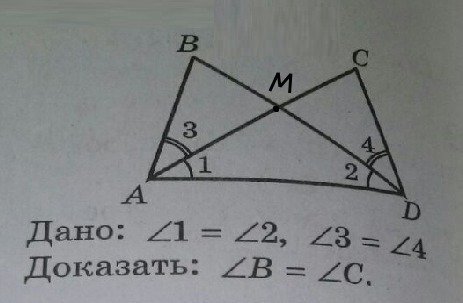
Обозначим точку пересечения АС и ВD буквой М. По условию в треугольнике АМD углы при основании АD равны. ⇒ ∆ АМD –равнобедренный, АМ=DM. Рассмотрим ∆ АВМ и ∆ DBM. Они имеют по два равных угла, прилежащих к равным сторонам: углы 3 и 4 равны по условию, углы при М равны как вертикальные, АМ=DM по доказанному. ∆ АВМ=∆ DCM по второму признаку равенства. В равных треугольниках сходственные элементы равны. поэтому угол В=углу С. Доказано.
Приложения:
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад