СССССССССрочно помогите решить задачу 70 балов По різні боки від центра круга радіус якого 3 см, проведені дві паралельні хорди(не рівні) однв з хорд є стороною правильного квадрата вписаного в це коло, а друга стороною правильного вписаного трикутника. Знайти площу частини кола розміщеного між хордами.
Ответы
Ответ дал:
0
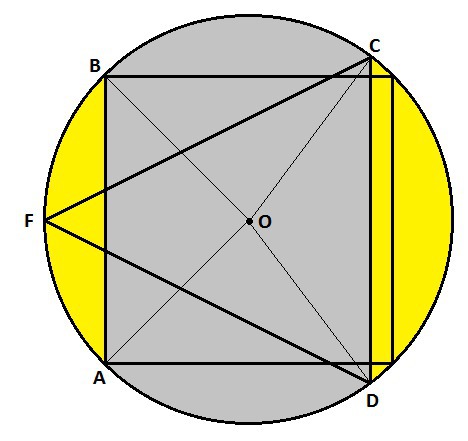
См. рисунок.
AB - одна хорда (сторона квадрата).
CD - другая хорда (сторона правильного треугольника).
Площадь части окружности между хордами (серый цвет) равна разности площади всей окружности и площади сегментов, образованных этими хордами (жёлтый цвет).
У квадрата диагонали пересекаются в точке О под прямым углом. Значит угол AOB = 90 градусов = . Тогда площадь левого сектора
. Тогда площадь левого сектора

У равностороннего треугольника все углы равны 60 градусов. Угол DFC = половине угла COD как вписанный. Значит, угол COD = 120 градусов = . Тогда площадь правого сегмента
. Тогда площадь правого сегмента

Тогда искомая площадь будет равна

AB - одна хорда (сторона квадрата).
CD - другая хорда (сторона правильного треугольника).
Площадь части окружности между хордами (серый цвет) равна разности площади всей окружности и площади сегментов, образованных этими хордами (жёлтый цвет).
У квадрата диагонали пересекаются в точке О под прямым углом. Значит угол AOB = 90 градусов =
У равностороннего треугольника все углы равны 60 градусов. Угол DFC = половине угла COD как вписанный. Значит, угол COD = 120 градусов =
Тогда искомая площадь будет равна
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад