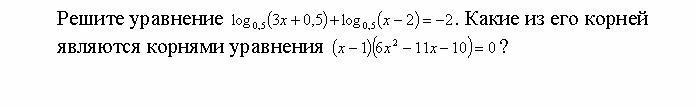Ответы
Ответ дал:
0
Есть только один корень 1 уравнения, совпадающий с корнем 2 уравнения . Это х=2,5 .
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад