Question

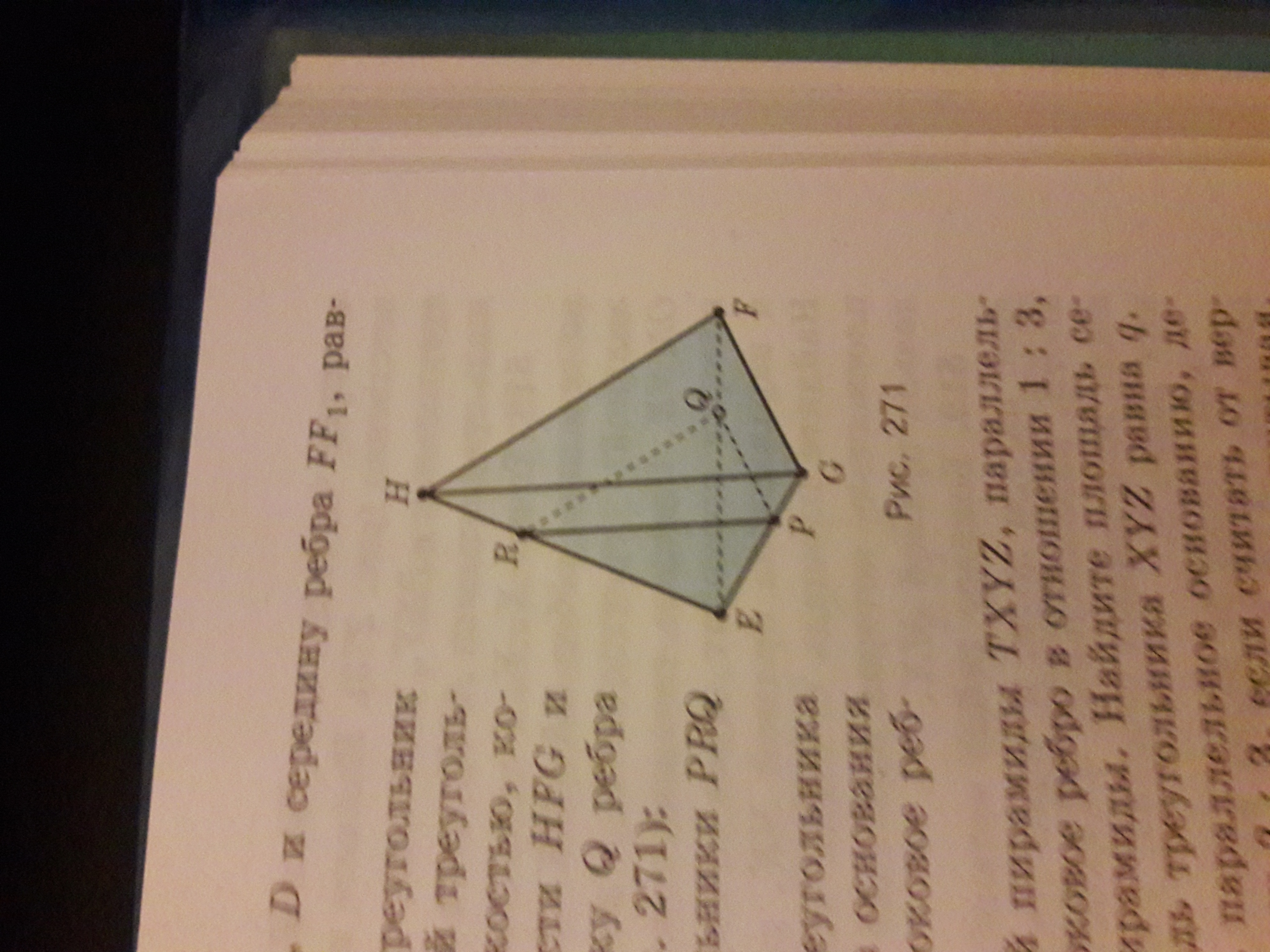
учитывая, что треугольник PRQ-сечение правильной треугольной пирамиды HEFG плоскостью, которая проходит через такую точку Q ребра FE, что FQ:QE=1:2
А) докажите, что треугольник PRQ и GHF подобны.
Б) найдите периметр треугольника PRQ, учитывая, что сторона основания пирамиды равна 30 см, а боковое ребро-90 см.

Answer 1

Самое главное - в условии не написано, что сечение PQR || FGH.
И, поэтому, доказать подобность треугольников сложно.
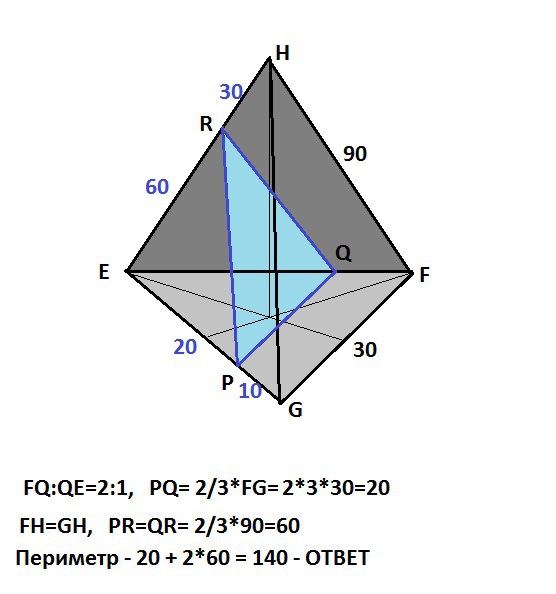
В этом случае вс е стороны делятся в заданном отношении 2:1.
PQ = 2/3*30 = 20
RQ = 2/3*90 = 60
Периметр сечения - 20 + 2*60 = 140 - ОТВЕТ