Ответы
Ответ дал:
0
√12=2√3
(1/3)·sin3x > 1/√12;
·sin3x > 3/√12;
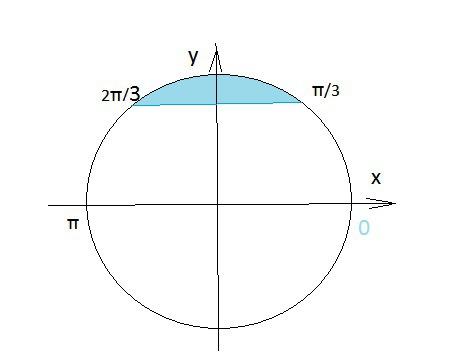
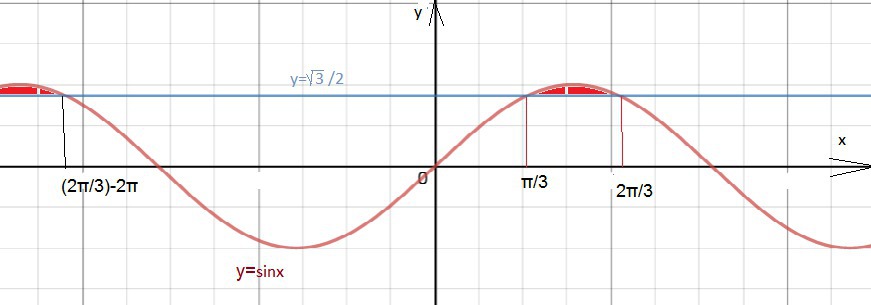
sin3x> √3/2
(π/3)+2πk < x < (2π/3) + 2πk, k ∈ Z.
Cм. решение на единичной окружности
и на графике
(1/3)·sin3x > 1/√12;
·sin3x > 3/√12;
sin3x> √3/2
(π/3)+2πk < x < (2π/3) + 2πk, k ∈ Z.
Cм. решение на единичной окружности
и на графике
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад