Из вершины А прямоугольного треугольника АВС угол С=90°,проведен перпендикуляр AD к его плоскости. Найти расстояние от точки D до катета BC. Если ВС=6см, DB=10см
Ответы
Ответ дал:
0
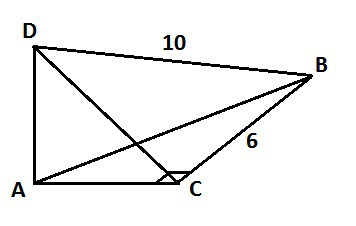
(см. рис.)
Проведём отрезок DC. Так как AD - перпендикуляр, плоскость ACD перпендикулярна плоскости ABC. Значит, расстоянием от точки D до катета BС будет отрезок DC.
Рассмотрим треугольник BCD. Так как плоскости ACD и ABC перпендикулярны, угол DCB прямой, а треугольник BCD - прямоугольный. Тогда по т. Пифагора
DC = √(DB^2-BC^2) = √(100-36) = √(64) = 8 см.
Проведём отрезок DC. Так как AD - перпендикуляр, плоскость ACD перпендикулярна плоскости ABC. Значит, расстоянием от точки D до катета BС будет отрезок DC.
Рассмотрим треугольник BCD. Так как плоскости ACD и ABC перпендикулярны, угол DCB прямой, а треугольник BCD - прямоугольный. Тогда по т. Пифагора
DC = √(DB^2-BC^2) = √(100-36) = √(64) = 8 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад
10 лет назад