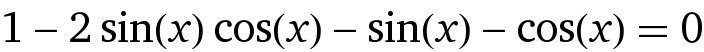Ответы
Ответ дал:
0
1-sin2x-sinx-cosx=0
1-sin2x-(sinx+cosx)=0
sinx+cosx=t замена
(sinx+cosx)^2=t^2
1+sin2x=t^2
sin2x=t^2-1
1-t^2-1-t=0
-t^2-t=0
t(-t-1)=0
t=0 t=-1
sinx+cosx=0| :cosx
tgx+1=0
tgx=-1
x=-п/4+пn,n€z
sinx+cosx=-1 |:√2
1/√2sinx+1/√2cosx=-1/√2
cosп/4sinx+sinп/4cosx=-1/√2
sin(п/4+х)=-1/√2
п/4+х=(-1)^n+1 *п/4 + пn,n€z
x=-п/4+(-1)^n+1*п/4+пn,n€z
1-sin2x-(sinx+cosx)=0
sinx+cosx=t замена
(sinx+cosx)^2=t^2
1+sin2x=t^2
sin2x=t^2-1
1-t^2-1-t=0
-t^2-t=0
t(-t-1)=0
t=0 t=-1
sinx+cosx=0| :cosx
tgx+1=0
tgx=-1
x=-п/4+пn,n€z
sinx+cosx=-1 |:√2
1/√2sinx+1/√2cosx=-1/√2
cosп/4sinx+sinп/4cosx=-1/√2
sin(п/4+х)=-1/√2
п/4+х=(-1)^n+1 *п/4 + пn,n€z
x=-п/4+(-1)^n+1*п/4+пn,n€z
Ответ дал:
0
всё верно
Ответ дал:
0
там единицы сокращаются
Ответ дал:
0
а нет , всё минус точно
Ответ дал:
0
не правильно , ну этот тип один из самых тугих
Ответ дал:
0
Ничего, мы справились)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад