Ответы
Ответ дал:
0
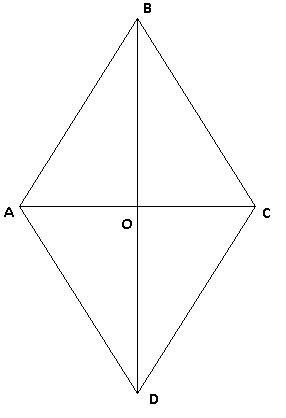
Диагонали ромба взаимно перпендикулярны.  ,
,  . Диагонали точкой О делятся пополам, т.е.
. Диагонали точкой О делятся пополам, т.е.  и
и  . Вычислив сторону АО по т. Пифагора из прямоугольного треугольника AOB, получим
. Вычислив сторону АО по т. Пифагора из прямоугольного треугольника AOB, получим  . Тогда диагональ АС равен
. Тогда диагональ АС равен 
Вычислив площадь ромба по формуле , получим
, получим  кв.ед.
кв.ед.
Ответ: 480 кв.ед.
Вычислив площадь ромба по формуле
Ответ: 480 кв.ед.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад