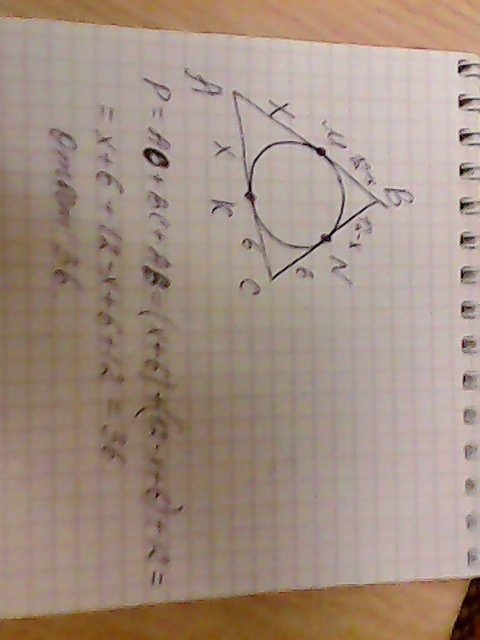
Пусть M, N, K - точки касания сторон треугольника A, B, C с окружностью такие, что M принадлежит [AB], N принадлежит [BC], K принадлежит [AC]. Найдите периметр треугольника ABC, если:
AB=12 см, KC=6 см.
х должен получиться 3, а периметр должен выйти 36 см
AM=AK=x см
ВM=BN=12-x см
NC=KC=6 см
Ответы
Ответ дал:
0
все верно, см.рисунок. По теореме об отрезках касательных, проведенных из одной точки получается:
AM=AK=x см
ВM=BN=12-x см
NC=KC=6 см
АВ=12, ВС=BN+NC=12-x+6. AC=x+6
Р=АС+ВС+АВ= x+6+12-x+6+12=36
AM=AK=x см
ВM=BN=12-x см
NC=KC=6 см
АВ=12, ВС=BN+NC=12-x+6. AC=x+6
Р=АС+ВС+АВ= x+6+12-x+6+12=36
Приложения:
Ответ дал:
0
спасибо!!!
Ответ дал:
0
можно фото по-лучше?
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад