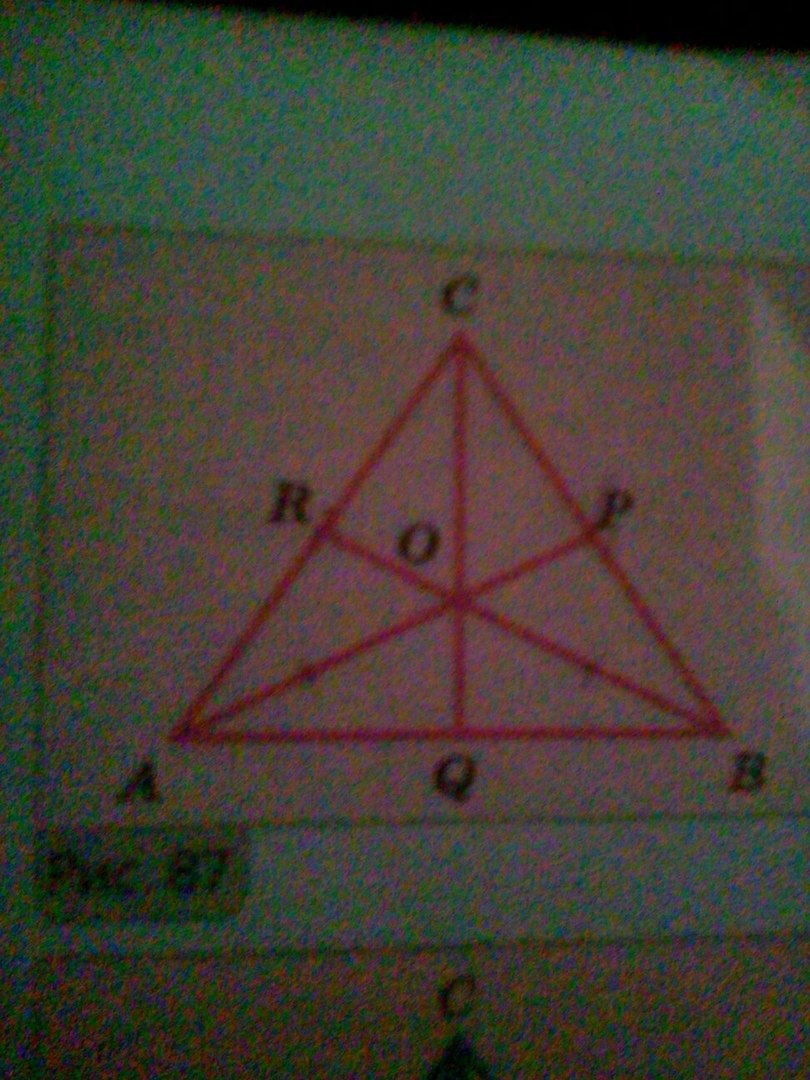
на этом рисунке AC=BCи AR=BP докажите что AP=BR равный
скажите пожалуйста просто только начали не очень понятно
Приложения:
Ответы
Ответ дал:
0
Так как АС=ВС, то ΔАВС - равнобедренный.
Значит ∠САВ=∠СВА (по свойству равнобедренного треугольника)
{напомню свойство:
углы при основании равнобедренного
треугольника равны}
ΔABR=ΔBAP (по I признаку равенства треугольников),
{по двум сторонам и углу между ними}
так как AR=ВР, АВ - общая сторона, ∠ВАR=∠AВP. {∠BAR=∠CAB находится между сторонами AR и AB,
∠AВP=∠СВА между BP и AB}
Отсюда следует, что AP=BR {Так в равных треуг. все соответствующие стороны и углы равны}
Что и требовалось доказать.
Значит ∠САВ=∠СВА (по свойству равнобедренного треугольника)
{напомню свойство:
углы при основании равнобедренного
треугольника равны}
ΔABR=ΔBAP (по I признаку равенства треугольников),
{по двум сторонам и углу между ними}
так как AR=ВР, АВ - общая сторона, ∠ВАR=∠AВP. {∠BAR=∠CAB находится между сторонами AR и AB,
∠AВP=∠СВА между BP и AB}
Отсюда следует, что AP=BR {Так в равных треуг. все соответствующие стороны и углы равны}
Что и требовалось доказать.
Ответ дал:
0
класс спс я тка и думал только как выразить не понял спс
Ответ дал:
0
Пожалуйста.
Ответ дал:
0
)))))))))))))
Вас заинтересует
7 лет назад
10 лет назад
10 лет назад