даны точки М1(3;-1;2) М2(4;-2;-1) составить уравнение плоскости проходящей через точку М1 перпендикулярно М1М2 и построить эту плоскость. 30 баллов
Ответы
Ответ дал:
0
Координаты вектора M₁M₂ :
- уравнение плоскости, проходящей через заданную точку, перпендикулярно вектору
В нашем случае вектор нормали и точка
. Подставляем их координаты, мы получим
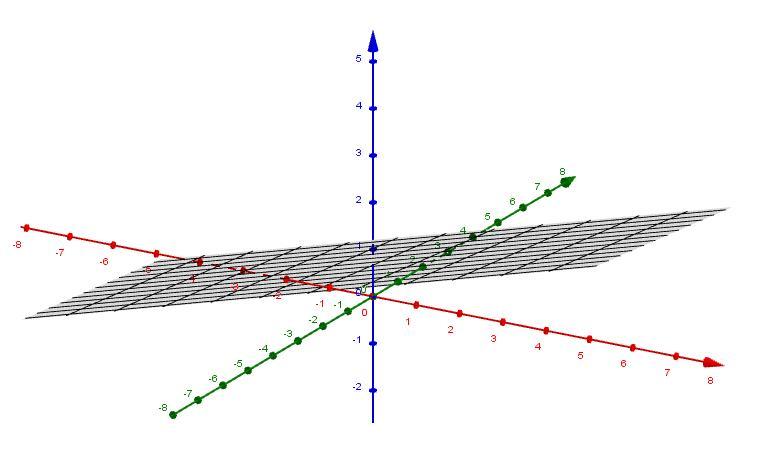
Последнее уравнение это искомое уравнение плоскости.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад